
【题目】已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与
与![]() 轴正半轴、
轴正半轴、![]() 轴围成的
轴围成的![]() 的面积为
的面积为![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求点![]() 坐标并判断
坐标并判断![]() 的形状,说明理由;
的形状,说明理由;
(3)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的面积为
的面积为![]() ,求
,求![]() 点坐标.
点坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;直角三角形;(3)
;直角三角形;(3)![]() 或
或![]()
【解析】
(1)根据待定系数法即可求得;
(2)根据△BOC的面积求得C的坐标,然后根据勾股定理求得AC,AB、BC的长,根据勾股定理的逆定理即可判定△ABC是直角三角形;
(3)设P(x,0),则AP=|x+4|,根据三角形面积公式即可得到![]() ,解得即可.
,解得即可.
(1)设直线l1的解析式为y=kx+b,
∵直线l1,与x轴交于点A(-4,0),与直线l2相交于点B(0,3)
∴![]()
解得![]()
∴直线l1的解析式为![]()
故答案为:![]()
(2)设C(m,0),![]() ,
,
∵△BOC的面积为![]()
∴![]()
即![]()
解得m=![]()
∴C(![]() ,0),
,0),
∴AC=4+![]() =
=![]()
则AC2=![]()
∵AB2=32+42=25,BC2=(![]() )2+32=
)2+32=![]()
∴AB2+BC2=25+![]() =
=![]()
∴AB2+BC2=AC2,
∴△ABC是直角三角形;
故答案为:直角三角形,理由见解析
(3)设P(x,0),则AP=|x+4|,
∵△BAP的面积为9,![]() APOB=9,即
APOB=9,即
![]() |x-4|×3=9,
|x-4|×3=9,
解得x1=2,x2=-10,
∴P点的坐标为(2,0)或(-10,0)
故答案为: (2,0)或(-10,0)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.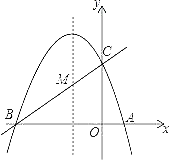
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y= ![]() (x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE= ![]() ,则BN的长为 .
,则BN的长为 . 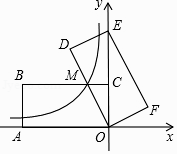
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )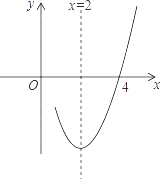
A.①②③
B.③④⑤
C.①②④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把以下证明过程补充完整:
已知:如图,∠A=∠F,∠C=∠D.点B,E分别在线段AC,DF上,对∠1=∠2进行说理.

理由:∵∠A=∠F(已知)
∴______∥FD (______)
∴∠D=______(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代换)
∴______∥______(同位角相等,两直线平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=![]() .其中所有正确结论的个数是( )
.其中所有正确结论的个数是( )

A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com