
【题目】某市2018年举行迎新春首届灯展,承办方计划在现场安装小彩灯和大彩灯,已知:安装5个小彩灯和4个大彩灯共需155元;安装7个小彩灯和6个大彩灯共需225元.
(1)安装1个小彩灯和1个大彩灯各需多少元.
(2)若承办方安装小彩灯和大彩灯的数量共300个,费用不超过5000元,则最多安装大彩灯多少个?
【答案】(1):安装1个小彩灯需要15元,安装1个大彩灯需要20元;(2)最多安装大彩灯100个.
【解析】
(1)设安装1个小彩灯需要x元,安装1个大彩灯需要y元,根据“安装5个小彩灯和4个大彩灯共需155元;安装7个小彩灯和6个大彩灯共需225元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设安装大彩灯z个,则安装小彩灯(300﹣z)个,根据安装费用不超过5000元,即可得出关于z的一元一次不等式,解之取其中的最大值即可得出结论.
解:(1)设安装1个小彩灯需要x元,安装1个大彩灯需要y元,
根据题意得:![]() ,
,
解得:![]() ,
,
答:安装1个小彩灯需要15元,安装1个大彩灯需要20元.
(2)设安装大彩灯z个,则安装小彩灯(300﹣z)个,
根据题意得:20z+15(300﹣z)≤5000,
解得:z≤100.
答:最多安装大彩灯100个.


科目:初中数学 来源: 题型:
【题目】某学校组织教师为地震救灾捐款,分6个工会小组进行统计,其中第6工会小组尚未统计在内,如图:
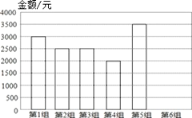
(1)求前5个工会小组捐款金额的众数、中位数和平均数;
(2)若全部6个小组的捐款平均数为2750元,求第6小组的捐款金额,并补全统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把以下证明过程补充完整:
已知:如图,∠A=∠F,∠C=∠D.点B,E分别在线段AC,DF上,对∠1=∠2进行说理.

理由:∵∠A=∠F(已知)
∴______∥FD (______)
∴∠D=______(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代换)
∴______∥______(同位角相等,两直线平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中:①m2是有理数;②m的值满足m2﹣12=0;③m满足不等式组![]() ;④m是12的算术平方根. 正确有几个( )
;④m是12的算术平方根. 正确有几个( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=![]() .其中所有正确结论的个数是( )
.其中所有正确结论的个数是( )

A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房. 如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)工厂补充10名新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置,则补充新工人后每天能配套生产多少产品?
(3)为了在规定期限内完成总任务,请问至少需要补充多少名(2)中的新工人才能在规定期内完成总任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技发展,社会进步.中国己进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗.青少年时期是良好品格形成和知识积累的黄金时期.为此,大数据平台针对部分中学生品格表现和学习状况进行统计词查绘制如下统计图表,请根据图中提供的信息解决下列问题,类别:A.品格健全,成绩优异:B.尊敬师长,积极进取:C.自控力差,被动学习:D.沉迷奢玩,消极自卑
(1)本次调查被抽取的样本容量为 ;
(2)“自控力差,被动学习”的同学有 人,并补全条形统计图;
(3)样本中D类所在扇形的圆心角为 度;
(4)试根据你所在学校的总人数,估算D类学生人数,并谈谈你的想法.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com