
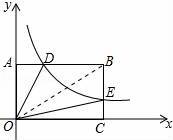
如图,在平面直角坐标系中,反比例函数y=
 (x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k= .
(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k= .


3 .
【考点】反比例函数系数k的几何意义.
【专题】压轴题.
【分析】连接OB,由矩形的性质和已知条件得出△OBD的面积=△OBE的面积=
 四边形ODBE的面积=3,在求出△OCE的面积,即可得出k的值.
四边形ODBE的面积=3,在求出△OCE的面积,即可得出k的值.
【解答】解:连接OB,如图所示:
∵四边形OABC是矩形,
∴∠OAD=∠OCE=∠DBE=90°,△OAB的面积=△OBC的面积,
∵D、E在反比例函数y=
 (x>0)的图象上,
(x>0)的图象上,
∴△OAD的面积=△OCE的面积,
∴△OBD的面积=△OBE的面积=
 四边形ODBE的面积=3,
四边形ODBE的面积=3,
∵BE=2EC,∴△OCE的面积=
 △OBE的面积=
△OBE的面积=
 ,
,
∴k=3;
故答案为:3.

【点评】本题考查了矩形的性质、三角形面积的计算、反比例函数的图象与解析式的求法;熟练掌握矩形的性质和反比例函数解析式的求法是解决问题的关键.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
某班同学到离校24千米的农场参观,一部分骑自行车的同学先走,1小时后,没有自行车的同学乘汽车出发,结果他们同时到达农场,已知汽车速度是自行车速度的3倍,求两种车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
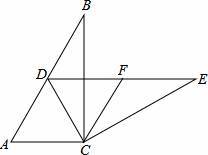
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系中,直线AB经点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,△AOB的内切圆的半径是( )


A.2 B.3.5 C.
 D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
把代数式ax2﹣4ax+4a分解因式,下列结果中正确的是( )
A.a(x﹣2)2 B.a(x+2)2 C.a(x﹣4)2 D.a(x+2)(x﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com