Question

如图，在直角坐标系中，直线AB经点P（3，4），与坐标轴正半轴相交于A，B两点，当△AOB的面积最小时，△AOB的内切圆的半径是（　　）                                                                         

                                                                          

A．2                            B．3.5                          C．              D．4

　                                                                                                      

Answer 1

A【考点】三角形的内切圆与内心；坐标与图形性质．                                   

【专题】压轴题；探究型．                                                                     

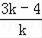
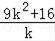
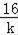
【分析】设直线AB的解析式是y=kx+b，把P（3，4）代入求出直线AB的解析式是y=kx+4﹣3k，求出OA=4﹣3k，OB=，求出△AOB的面积是OBOA=12﹣=12﹣（9k+），根据﹣9k﹣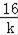≥2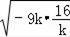=24和当且仅当﹣9k=﹣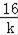时，取等号求出k=﹣，求出OA=4﹣3k=8，OB=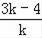=6，设三角形AOB的内切圆的半径是R，由三角形面积公式得：×6×8=×6R+×8R+×10R，求出即可．                                               

【解答】解：设直线AB的解析式是y=kx+b，                                         

把P（3，4）代入得：4=3k+b，                                                              

b=4﹣3k，                                                                                          

即直线AB的解析式是y=kx+4﹣3k，                                                       

当x=0时，y=4﹣3k，                                                                        

当y=0时，x=，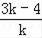                                                                            

即A（0，4﹣3k），B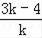（，0），                                                    

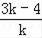
△AOB的面积是OBOA=（4﹣3k）=12﹣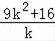=12﹣（9k+），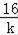                   

∵要使△AOB的面积最小，                                                                     

∴必须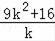最大，                                                                       

∵k＜0，                                                                                            

∴﹣k＞0，                                                                                        

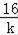
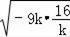
∵﹣9k﹣≥2=2×12=24，                                                     

当且仅当﹣9k=﹣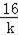时，取等号，解得：k=±，                                            

∵k＜0，                                                                                            

∴k=﹣，                                                                                         

即OA=4﹣3k=8，OB=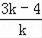=6，                                                            

根据勾股定理得：AB=10，                                                                      

设三角形AOB的内切圆的半径是R，                                                      

由三角形面积公式得：×6×8=×6R+×8R+×10R，                                    

R=2，                                                                                                

故选A．                                                                                            

【点评】本题考查了勾股定理，取最大值，三角形的面积，三角形的内切圆等知识点的应用，关键是求OA和OB的值，本题比较好，但是有一定的难度．