
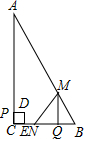
 如图,在Rt△ABC中,AC=24cm,BC=12cm,动点P从点C出发,以1cm/s的速度沿CA方向向点A运动,同时点Q从点B出发,以1.5cm/s的速度沿BC方向向点C运动,当点Q到达终点时,点P也随之停止运动,过点Q作QM⊥BC,交AB于点M,以线段MQ为直角边在MQ的左侧作等腰直角△MQN,以线段CP为一边在△ABC内部作正方形PDEC,设运动时间为t(s),△MQN与正方形PDEC重叠部分的面积为S(cm2).
如图,在Rt△ABC中,AC=24cm,BC=12cm,动点P从点C出发,以1cm/s的速度沿CA方向向点A运动,同时点Q从点B出发,以1.5cm/s的速度沿BC方向向点C运动,当点Q到达终点时,点P也随之停止运动,过点Q作QM⊥BC,交AB于点M,以线段MQ为直角边在MQ的左侧作等腰直角△MQN,以线段CP为一边在△ABC内部作正方形PDEC,设运动时间为t(s),△MQN与正方形PDEC重叠部分的面积为S(cm2).分析 (1)如图1,P在MN上,先表示两动点的路程:PC=t,BQ=1.5t,证明△MQB∽△ACB,列比例式可表示MQ=3t,根据NQ=3t列方程可求得t的值;
如图2,点D在MQ上,根据CE=CQ列式求得t的值;
(2)分四种情况:
①当N与C重合时,如图3,此时t=$\frac{8}{3}$s,△MQN与正方形PDEC重叠部分△CDE,根据面积公式求得S;
②当$\frac{8}{3}$<t<$\frac{24}{7}$时,如图4,△MQN与正方形PDEC重叠部分是五边形GHCED,根据S=S正方形PCED-S△PGH可得结论;
③当$\frac{24}{7}$$≤t≤\frac{24}{5}$时,如图5,△MQN与正方形PDEC重叠部分是正方形PCED;
④当$\frac{24}{5}$<t≤8时,如图6,△MQN与正方形PDEC重叠部分是矩形PCQG;
(3)线段FG扫过的图形面积是△BFG的面积,分别求GF和FC的长,代入面积公式计算即可.
解答  解:(1)当P在MN上时,如图1,
解:(1)当P在MN上时,如图1,
由题意得:PC=t,BQ=1.5t,
∵△MQN是等腰直角三角形,
∴MQ=NQ,∠NQM=90°,∠MNQ=45°,
∵∠ACB=90°,
∴∠ACB+∠NQM=180°,
∴AC∥MQ,
∴△MQB∽△ACB,
∴$\frac{MQ}{AC}=\frac{BQ}{BC}$,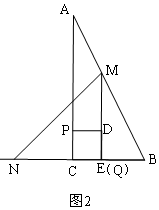
∴$\frac{MQ}{24}=\frac{1.5t}{12}$,
∴MQ=3t,
∴NQ=MQ=3t,
∵△PCN是等腰直角三角形,
∴NC=PC=t,
∴NC+CQ=NQ,
t+12-1.5t=3t,
t=$\frac{24}{7}$,
即当点P在MN上时,t=$\frac{24}{7}$s;
当点D在MQ上时,如图2,此时Q与E重合,
由题意得:CE=PC=t,CQ=12-1.5t,
∴t=12-1.5t,
t=$\frac{24}{5}$,
即当点D在MQ上时,t=$\frac{24}{5}$s;
故答案为:$\frac{24}{7}$;$\frac{24}{5}$;
(2)①当N与C重合时,如图3,
∵四边形PCDE是正方形,
∴∠DCE=45°,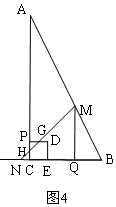
∵△MNQ是等腰直角三角形,
∴∠MNQ=45°,
∴此时D在CM上,
则CQ+BQ=BC,
3t+1.5t=12,
9t=24,
t=$\frac{8}{3}$;
此时,△MQN与正方形PDEC重叠部分是△CDE,
S=S△CDE=$\frac{1}{2}$CE•ED=$\frac{1}{2}{t}^{2}$=$\frac{1}{2}$×$(\frac{8}{3})^{2}$=$\frac{32}{9}$;
②当$\frac{8}{3}$<t<$\frac{24}{7}$时,如图4,△MQN与正方形PDEC重叠部分是五边形GHCED,
此时,CQ=12-1.5t,NC=3t+1.5t-12=4.5t-12,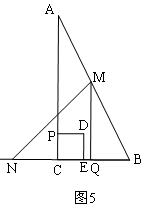
∵∠MNQ=45°,
∴△NCH是等腰直角三角形,
∴NC=HC=4.5t-12,
∴PH=PG=t-(4.5t-12)=12-3.5t,
∴S=S正方形PCED-S△PGH=t2-$\frac{1}{2}$(12-3.5t)2=-$\frac{41}{8}{t}^{2}$+42t-72;
③当$\frac{24}{7}$$≤t≤\frac{24}{5}$时,如图5,△MQN与正方形PDEC重叠部分是正方形PCED,
此时S=$\frac{1}{2}{t}^{2}$;
④当$\frac{24}{5}$<t≤8时,如图6,△MQN与正方形PDEC重叠部分是矩形PCQG,
CQ=12-1.5t,
∴S=S矩形PCQE=PC•CQ=t(12-1.5t)=-1.5t2+12t;
综上所述,当$\frac{8}{3}$≤t≤8时,S与t之间的函数关系是:
S=$\left\{\begin{array}{l}{\frac{32}{9}(t=\frac{8}{3})}\\{-\frac{41}{8}{t}^{2}+42t-72(\frac{8}{3}<t<\frac{24}{7})}\\{\frac{1}{2}{t}^{2}(\frac{24}{7}≤t≤\frac{24}{5})}\\{-1.5{t}^{2}+12t(\frac{24}{5}<t≤8)}\end{array}\right.$;
(3)如图7,在整个运动过程中,线段FG扫过的图形面积是图中阴影部分的面积,即△BFG的面积,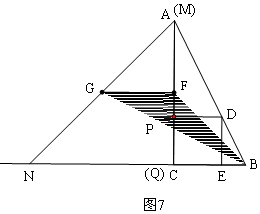
此时Q与C重合,
∴NC=AC=24,
∵点F、G分别是MQ、MN的中点,
∴GF是△ANC的中位线,
∴GF∥NC,GF=$\frac{1}{2}$NC=$\frac{1}{2}$AC=12,
FC=$\frac{1}{2}$AC=12,
∴S△BFG=$\frac{1}{2}$GF•FC=$\frac{1}{2}$×12×12=72;
则线段FG扫过的图形面积是72cm2.
点评 本题是四边形的综合题,考查了正方形的性质、等腰直角三角形的性质和判定、动点运动问题、三角形相似的性质和判定,还有重叠部分面积问题,有难度,尤其是第二问,要利用数形结合的思想,注意重叠部分图形的不同,并与函数相结合,解决问题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{11}$ | B. | $\frac{1}{11}$ | C. | -$\frac{5}{7}$ | D. | -$\frac{7}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
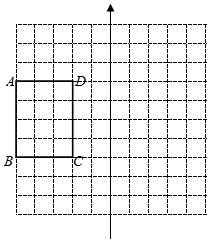 如图,已知长方形ABCD在平面直角坐标系(x轴和原点O均未画出)中,网格图中每个小正方形的边长都是1个单位长度,已知长方形ABCD在平面直角坐标系中关于x轴对称.
如图,已知长方形ABCD在平面直角坐标系(x轴和原点O均未画出)中,网格图中每个小正方形的边长都是1个单位长度,已知长方形ABCD在平面直角坐标系中关于x轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com