
【题目】综合:
(1)在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系. 小亮同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF、FD之间的数量关系.请你按照小亮的思路写出推理过程.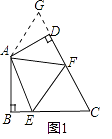
(2)如图2,已知正方形ABCD,△AEF是正方形ABCD的内接等边三角形,请你找出S△ABE、S△ADF、S△CEF之间的数量关系,并说明理由. 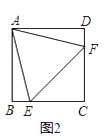
【答案】
(1)解:延长FD到点G,使DG=BE,连接AG,
在△ABE和△ADG中,
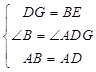 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF= ![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF.
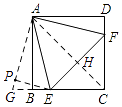
(2)解:S△CEF=S△ABE+S△ADF,理由如下:
如图,延长EB至G,使得BG=DF,连接AC,交EF于H,过E作EP⊥AG,
∵四边形ABCD是正方形,
∴AB=AD,∠ABG=∠D,
在△ABG和△ADF中,
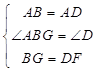 ,
,
∴△ABG≌△ADF(SAS),
∴BE=DF,∠DAF=∠BAG,AG=AF,
∴CE=CF,
又∵AE=AF,
∴AC垂直平分EF,且△CEF是等腰直角三角形,
设EF=2,则EH=CH=1,AE=AG=2,
∴S△CEF= ![]() EF×CH=1,
EF×CH=1,
∵∠EAG=∠BAG+∠BAE=∠DAF+∠BAE=90°﹣60°=30°,
∴PE= ![]() AE=1,
AE=1,
∴S△AGE= ![]() AG×PE=1,
AG×PE=1,
∴S△CEF=S△AGE,
即S△CEF=S△ABE+S△ABG=S△ABE+S△ADF.
【解析】(1)延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到BE、EF、FD之间的数量关系.(2)延长EB至G,使得BG=DF,连接AC,交EF于H,过E作EP⊥AG,构造全等三角形,再求得S△CEF= ![]() EF×CH=1,S△AGE=
EF×CH=1,S△AGE= ![]() AG×PE=1,即可得到S△CEF=S△AGE,即S△CEF=S△ABE+S△ABG=S△ABE+S△ADF.
AG×PE=1,即可得到S△CEF=S△AGE,即S△CEF=S△ABE+S△ABG=S△ABE+S△ADF.
【考点精析】利用等边三角形的性质和正方形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知一次函数的图象经过点(2,3)与(﹣3,﹣7).
(1)求这个一次函数的解析式;
(2)求这个一次函数的图象与x轴、y轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣2x+a与y轴交于点C (0,6),与x轴交于点B. 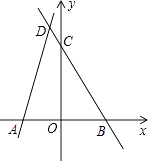
(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(﹣1,n),点A的坐标为(﹣3,0). ①求n的值及直线AD的解析式;
②求△ABD的面积;
③点M是直线y=﹣2x+a上的一点(不与点B重合),且点M的横坐标为m,求△ABM的面积S与m之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
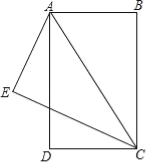
【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 ,可使四边形ABCD为矩形.请加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com