
【题目】如图, ![]() 是
是![]() 的直径,
的直径, ![]() ,连接
,连接![]() .
.

(1)求证: ![]() ;
;
(2)若直线![]() 为
为![]() 的切线,
的切线, ![]() 是切点,在直线
是切点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() 所在的直线与
所在的直线与![]() 所在的直线相交于点
所在的直线相交于点![]() ,连接
,连接![]() .
.
①试探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
②![]() 是否为定值?若是,请求出这个定值;若不是,请说明理由.
是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)证明见解析;(2)①![]() , ②
, ②![]() .
.
【解析】试题分析:(1)根据直径所对的圆周角是直角,等弧所对的圆周角是圆心角的一半即可进行证明;
(2)根据题意画出图形,
①要分两种情况进行讨论,通过证明∠ADE=∠AED即可得;
②结合(2)中的不同情况,通过证明△ACD与△ABE相似,再结合△IBE即可求解.
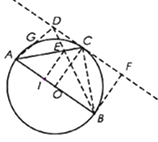
试题解析:(1)如图,连接BC,
∵AB是![]() 的直径,
的直径, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ;
;
(2)AD=AE,理由如下:
ⅰ如图所示,作![]() 于F,
于F,
由(1)可得, ![]() 为等腰直角三角形,
为等腰直角三角形,
![]() 是
是![]() 的中点,
的中点, ![]() ,
, ![]() 为等腰直角三角形,
为等腰直角三角形,
又![]() 是
是![]() 的切线,
的切线, ![]() ,
,
![]() ,
, ![]() 四边形
四边形![]() 为矩形 ,
为矩形 , ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ;
;
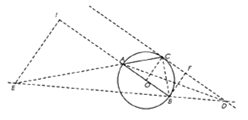
ⅱ当![]() 为钝角时,如图所示,同理,
为钝角时,如图所示,同理, ![]() ,
,
![]() ,
,
![]() ;
;
②是定值,
当D在C左侧时,由(2)知,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中, ![]() ,
,
![]() ,
,
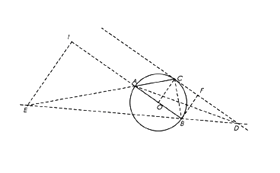
当D在C右侧时,过E作![]() 于
于![]() ,
,
由(2)得, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .说明
.说明![]() 的理由.
的理由.

解:因为![]() (已知),
(已知),
所以![]() ∥
∥![]() (________________________________).
(________________________________).
所以![]() (_____________________________).
(_____________________________).
因为![]() 平分
平分![]() (已知),
(已知),
所以![]() (_______________________________).
(_______________________________).
同理![]() .
.
所以![]() (___________________________________).
(___________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
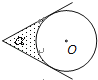
【题目】如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A. 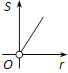 B.
B. 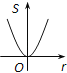 C.
C. 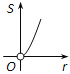 D.
D. 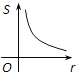
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 的对角线
的对角线![]() ,
, ![]() 相交于点
相交于点![]() ,
, ![]() 关于
关于![]() 的对称图形为
的对称图形为![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)连接![]() ,若
,若![]() ,
, ![]() .
.
①求![]() 的值;
的值;
②若点![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 重合),连接
重合),连接![]() ,一动点
,一动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿线段
的速度沿线段![]() 匀速运动到点
匀速运动到点![]() ,再以
,再以![]() 的速度沿线段
的速度沿线段![]() 匀速运动到点
匀速运动到点![]() ,到达点
,到达点![]() 后停止运动.当点
后停止运动.当点![]() 沿上述路线运动到点
沿上述路线运动到点![]() 所需要的时间最短时,求
所需要的时间最短时,求![]() 的长和点
的长和点![]() 走完全程所需的时间.
走完全程所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的面积为1.分别倍长(延长一倍)
的面积为1.分别倍长(延长一倍)![]() ,BC,CA得到
,BC,CA得到![]() .再分别倍长A1B1,B1C1,C1A1得到
.再分别倍长A1B1,B1C1,C1A1得到![]() .…… 按此规律,倍长2018次后得到的
.…… 按此规律,倍长2018次后得到的![]() 的面积为( )
的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一拱形公路桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.(1)求桥拱的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com