
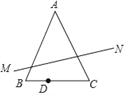
【题目】如图,△ABC中,AB=AC,∠BAC=45°,BC=2,D是线段BC上的一个动点,点D是关于直线AB、AC的对称点分别为M、N,则线段MN长的最小值是_____.
科目:初中数学 来源: 题型:
【题目】解:根据算术平方根的意义,由![]() ,得(2x-y)2=9,所以2x-y=3.①(第一步)
,得(2x-y)2=9,所以2x-y=3.①(第一步)
根据立方根的意义,由![]() ,得x-2y=-3.②(第二步)
,得x-2y=-3.②(第二步)
解得x=3,y=3.
把x、y的值代入分式中,得![]() .(第三步)
.(第三步)
上述解答有两处错误,一处是___________步,忽视了___________;另一处是步___________,忽视了___________.请写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.

(1)如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数;
(2)如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹);
(3)在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个车队共有20辆小轿车,正以每小时36千米的速度在一条笔直的街道上匀速行驶,行驶时车与车的间隔均相等,甲停在路边等人,他发现该车队从第一辆车的车头到最后一辆的车尾经过自己身边共用了20秒的时间,假设每辆车的车长均为4.87米.
(1)求行驶时车与车的间隔为多少米?
(2)若乙在街道一侧的人行道上与车队同向而行,速度为![]() 米/秒,当第一辆车的车头到最后一辆车的车尾经过他身边共用了40秒,求
米/秒,当第一辆车的车头到最后一辆车的车尾经过他身边共用了40秒,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高足球基本功,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)请用树状图列举出三次传球的所有可能情况;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.

(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数。例如:M{1,0,2}=![]() ;min{1,0,2}=1;min{1,0,a}=
;min{1,0,2}=1;min{1,0,a}=![]() .如果M{2,x+1,2x}=min{2,x+1,2x},则x的值是( )
.如果M{2,x+1,2x}=min{2,x+1,2x},则x的值是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.
(1)当t=2时,则AP= ,此时点P的坐标是 。
(2)当t=3时,求过点P的直线l:y=-x+b的解析式?
(3)当直线l:y=-x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com