
如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.


【考点】二次函数综合题.
【专题】代数几何综合题.
【分析】(1)把点A、B的坐标代入抛物线解析式,解方程组求出b、c的值,即可得解;
(2)令y=0,利用抛物线解析式求出点C的坐标,设点D的坐标为(0,m),作EF⊥y轴于点F,利用勾股定理列式表示出DC2与DE2,然后解方程求出m的值,即可得到点D的坐标;
(3)根据点C、D、E的坐标判定△COD和△DFE全等,根据全等三角形对应角相等可得∠EDF=∠DCO,然后求出CD⊥DE,再利用勾股定理求出CD的长度,然后①分OC与CD是对应边;②OC与DP是对应边;根据相似三角形对应边成比例列式求出DP的长度,过点P作PG⊥y轴于点G,再分点P在点D的左边与右边两种情况,分别求出DG、PG的长度,结合平面直角坐标系即可写出点P的坐标.
【解答】解:(1)∵抛物线y=x2+bx+c经过A(﹣1,0)、B(0,﹣3),
∴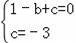
 ,
,
解得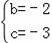
 ,
,
故抛物线的函数解析式为y=x2﹣2x﹣3;
(2)令x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
则点C的坐标为(3,0),
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴点E坐标为(1,﹣4),
设点D的坐标为(0,m),作EF⊥y轴于点F,
∵DC2=OD2+OC2=m2+32,DE2=DF2+EF2=(m+4)2+12,
∵DC=DE,
∴m2+9=m2+8m+16+1,
解得m=﹣1,
∴点D的坐标为(0,﹣1);
(3)∵点C(3,0),D(0,﹣1),E(1,﹣4),
∴CO=DF=3,DO=EF=1,
根据勾股定理,CD=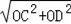
 =
=
 =
=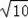
 ,
,
在△COD和△DFE中,
∵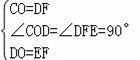
 ,
,
∴△COD≌△DFE(SAS),
∴∠EDF=∠DCO,
又∵∠DCO+∠CDO=90°,
∴∠EDF+∠CDO=90°,
∴∠CDE=180°﹣90°=90°,
∴CD⊥DE,
①分OC与CD是对应边时,
∵△DOC∽△PDC,
∴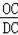
 =
=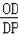
 ,
,
即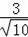
 =
=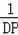
 ,
,
解得DP=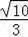
 ,
,
过点P作PG⊥y轴于点G,
则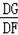
 =
=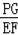
 =
=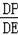
 ,
,
即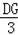
 =
=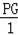
 =
=
 ,
,
解得DG=1,PG=
 ,
,
当点P在点D的左边时,OG=DG﹣DO=1﹣1=0,
所以点P(﹣
 ,0),
,0),
当点P在点D的右边时,OG=DO+DG=1+1=2,
所以,点P(
 ,﹣2);
,﹣2);
②OC与DP是对应边时,
∵△DOC∽△CDP,
∴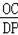
 =
=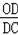
 ,
,
即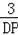
 =
=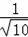
 ,
,
解得DP=3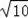
 ,
,
过点P作PG⊥y轴于点G,
则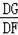
 =
=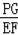
 =
=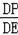
 ,
,
即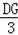
 =
=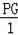
 =
=
 ,
,
解得DG=9,PG=3,
当点P在点D的左边时,OG=DG﹣OD=9﹣1=8,
所以,点P的坐标是(﹣3,8),
当点P在点D的右边时,OG=OD+DG=1+9=10,
所以,点P的坐标是(3,﹣10),
综上所述,满足条件的点P共有4个,其坐标分别为(﹣
 ,0)、(
,0)、(
 ,﹣2)、(﹣3,8)、(3,﹣10).
,﹣2)、(﹣3,8)、(3,﹣10).

【点评】本题考查了二次函数的综合题型,主要涉及待定系数法求二次函数解析式,勾股定理的应用,相似三角形对应边成比例的性质,(3)题稍微复杂,一定要注意分相似三角形的对应边的不同,点P在点D的左右两边的情况讨论求解.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
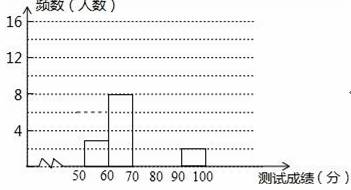
为了增强学生法律意识,某校举办了首届“法律进校园,法在我心中”知识大赛,经选拔后有25名学生参加决赛,这25名学生同时解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 3 |
| 第2组 | 60≤x<70 | 7 |
| 第3组 | 70≤x<80 | 10 |
| 第4组 | 80≤x<90 | m |
| 第5组 | 90≤x<100 | 2 |
(1)求表中m的值;
(2)请把频数分布直方图补充完整;
(3)第4组的同学将抽出2名对第一组2名同学进行“一帮一”辅导,则第4组的小王与小李能同时抽到的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=
 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com