
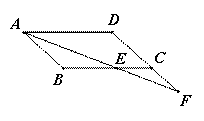
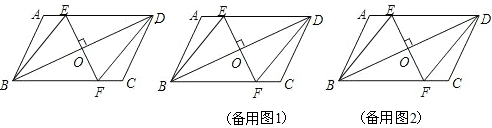
在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F。
(1)在图1中证明![]() ;
;
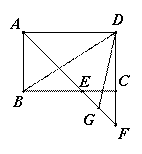
(2)若![]() ,G是EF的中点(如图2),直接写出∠BDG的度数;
,G是EF的中点(如图2),直接写出∠BDG的度数;
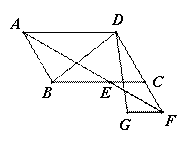
(3)若![]() ,FG∥CE,
,FG∥CE,![]() ,分别连结DB、DG(如图3),求∠BDG的度数。
,分别连结DB、DG(如图3),求∠BDG的度数。
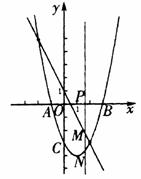
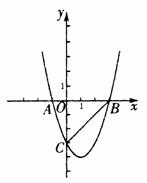
[解] (1) ∵ 点A、B是二次函数y=mx2+(m-3)x-3 (m>0)的图象与x轴的交点,
∴ 令y=0,即mx2+(m-3)x-3=0,解得x1= -1, x2=![]() ,又∵ 点A在点B左侧且m>0,
,又∵ 点A在点B左侧且m>0,
∴ 点A的坐标为(-1,0).
(2) 由(1)可知点B的坐标为(![]() ,0).
,0).
∵ 二次函数的图象与y轴交于点C,
∴ 点C的坐标为(0, -3).
∵ ÐABC=45°,∴![]() =3,∴m=1。
=3,∴m=1。
(3) 由(2)得,二次函数解析式为y=x2-2x-3.依题意并结合图象可知,一次函数的图象与二次函数的图象交点的横坐标分别为-2和2,由此可得交点坐标为(-2,5)和(2, -3).将交点坐标分别代入一次函数解析式y=kx+b中,得 -2k+b=5,且2k+b= -3,解得k= -2,b=1,
∴ 一次函数的解析式为y= -2x+1。


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
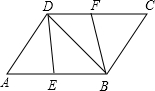 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com