
【题目】如图,在△ABC与△DBC中,∠ACB=∠DBC=90°,E是BC的中点,EF⊥AB,AB=DE.
(1)求证:BC=DB;
(2)若BD=8cm,求AC的长.

【答案】(1)见解析; (2)4
【解析】
(1)由DE⊥AB,可得∠BFE=90°,由直角三角形两锐角互余,可得∠ABC+∠DEB=90°,由∠ACB=90°,由直角三角形两锐角互余,可得∠ABC+∠A=90°,根据同角的余角相等,可得∠A=∠DEB,然后根据AAS判断△ABC≌△EDB,根据全等三角形的对应边相等即可得到BD=BC;
(2)由(1)可知△ABC≌△EDB,根据全等三角形的对应边相等,得到AC=BE,由E是BC的中点,得到BE=![]() .
.
(1)∵DE⊥AB,可得∠BFE=90°,
∴∠ABC+∠DEB=90°,
∵∠ACB=90°,
∴∠ABC+∠A=90°,
∴∠A=∠DEB,
在△ABC和△EDB中,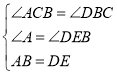 ,
,
∴△ABC≌△EDB(AAS),
∴BD=BC;
(2)∵△ABC≌△EDB,
∴AC=BE,
∵E是BC的中点,BD=8cm,
∴BE=![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,过D点作AB垂线,交AC于E,交BC的延长线于F.

(1)∠1与∠B有什么关系?说明理由.
(2)若BC=BD,请你探索AB与FB的数量关系,并且说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)阅读材料:分解因式:![]()
解:![]()
=![]()
=![]()
=![]()
=![]()
=![]() ,
,
此种方法抓住了二次项和一次项的特点,然后加一项,使三项成为完全平方式,我们把这种分解因式的方法叫配方法.
(1)用上述方法分解因式:![]() ;
;
(2)无论![]() 取何值,代数式
取何值,代数式![]() 总有一个最小值,请尝试用配方法求出当
总有一个最小值,请尝试用配方法求出当![]() 取何值时代数式的值最小,并求出这个最小值.
取何值时代数式的值最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面一元二次方程的解法中,正确的是( )
A. (x-3)(x-5)=10×2,∴x-3=10,x-5=2,∴x1=13,x2=7
B. (2-5x)+(5x-2)2=0,∴(5x-2)(5x-3)=0,∴x1=![]() ,x2=
,x2=![]()
C. (x+2)2+4x=0,∴x1=2,x2=-2
D. x2=x 两边同除以x,得x=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高港花卉中心销售一批兰花,每盆进价![]() 元,售价为
元,售价为![]() 元,平均每天可售出
元,平均每天可售出![]() 盆.为了扩大销量,该店决定适当降价.据调查,每盆兰花每降价
盆.为了扩大销量,该店决定适当降价.据调查,每盆兰花每降价![]() 元,每天可多售出
元,每天可多售出![]() 盆.
盆.
![]() 要使得每天利润达到
要使得每天利润达到![]() 元,则每盆兰花售价应定为多少元?
元,则每盆兰花售价应定为多少元?
![]() 如果该店每天兰花的进货成本不超过
如果该店每天兰花的进货成本不超过![]() 元,要使得每天利润达到
元,要使得每天利润达到![]() 元,则每盆兰花售价应定为多少元?
元,则每盆兰花售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH(线段端点在格点上),
⑴选取其中三条线段,使得这三条线段能围成一个直角三角形.
答:选取的三条线段为 .
⑵只变动其中两条线段的位置,在原图中画出一个满足上题的直角三角形(顶点仍在格点,并标上必要的字母).
答:画出的直角三角形为△ .
⑶所画直角三角形的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点E在BC边上,AE=AB,将线段AC绕A点旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)求证:EF=BC;
(2)若∠ABC=62°,∠ACB=29°,求∠FGC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()

![]() 求该抛物线的对称轴和顶点坐标;
求该抛物线的对称轴和顶点坐标;
![]() 求抛物线与
求抛物线与![]() 轴交点的坐标;
轴交点的坐标;
![]() 画出抛物线的示意图;
画出抛物线的示意图;
![]() 根据图象回答:当
根据图象回答:当![]() 在什么范围时,
在什么范围时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 在什么范围时,
在什么范围时,![]() 随
随![]() 的增大而减小?
的增大而减小?
![]() 根据图象回答:当
根据图象回答:当![]() 为何值时,
为何值时,![]() ;当
;当![]() 为何值时,
为何值时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com