
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH(线段端点在格点上),
⑴选取其中三条线段,使得这三条线段能围成一个直角三角形.
答:选取的三条线段为 .
⑵只变动其中两条线段的位置,在原图中画出一个满足上题的直角三角形(顶点仍在格点,并标上必要的字母).
答:画出的直角三角形为△ .
⑶所画直角三角形的面积为 .

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产
辆自行车,平均每天生产![]() 辆,由于各种原因实际每天生产量与计划相比有出入.下表是某一周的生产情况(超产为正,减产为负):
辆,由于各种原因实际每天生产量与计划相比有出入.下表是某一周的生产情况(超产为正,减产为负):
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产_________辆;
(2)产量最多的一天比产量最少的一天多生产__________辆;
(3)该厂实行周计划工作制,每辆车![]() 元,超额完成任务,超过的部分再奖励
元,超额完成任务,超过的部分再奖励![]() 元,完不成任务时,每少生产一辆扣
元,完不成任务时,每少生产一辆扣![]() 元,那么该厂工人这一周的工资总金额是多少?
元,那么该厂工人这一周的工资总金额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
如图 1,△ABC 中,沿∠BAC 的平分线 AB1 折叠,剪掉重叠部分;将余下部分沿∠B1A1C 的平分线 A1B2 折 叠,剪掉重叠部分;如此反复操作,沿 ∠Bn An C 的平分线 An Bn-1 折叠,点 Bn 与点 C 重合,我们就称 ∠BAC是△ABC 的正角.
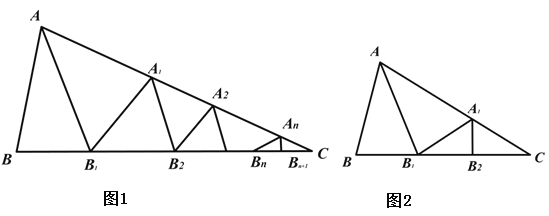
以图 2 为例,△ABC 中,∠B=70°,∠C=35°,若沿∠BAC 的平分线 AB1 折叠,则∠AA1B=70°.沿 A1B1 剪掉重叠部分,在余下的△B1A1C 中,由三角形的内角和定理可知∠A1B1C=35°,若沿∠B1A1C 的平分线 A1B2 第二次折叠,则点 B1 与点 C 重合. 此时,我们就称∠BAC 是△ABC 的正角.
探究发现
(1)△ABC 中,∠B= 2∠C ,则经过两次折叠后,∠BAC 是不是△ABC 的正角? (填“是”或“不是” ) .
(2)小明经过三次折叠发现∠BAC 是△ABC 的正角,则 ∠B 与∠C (不妨设 ∠B >∠C ) 之间的等量关系 为 .
根据以上内容猜想:若经过 n 次折叠 ∠BAC 是△ABC 的正角,则∠B 与 ∠C (不妨设∠B> ∠C ) 之间 的等量关系为 .
应用提升
(3)如果一个三角形的最小角是 10°,直接写出此三角形另外两个角的度数,使得此三角形的三个角均是 它的正角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上,从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t秒。
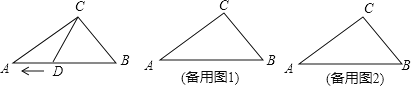
(1)点D在运动t秒后,BD= cm(用含有t的式子表示)
(2)AB=cm,AB边上的高为cm;
(3)点D在运动过程中,当△BCD为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
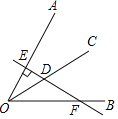
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB=12,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM?
(2)当P在线段AB上运动时,试说明2BM﹣BP为定值.
(3)当P在AB延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变,选择一个正确的结论,并求出其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知变量x、y对应关系如下表已知值呈现的对应规律.
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | 4 | … |
y | … |
|
| 1 | 2 | ﹣2 | ﹣1 | ﹣ | ﹣ | … |
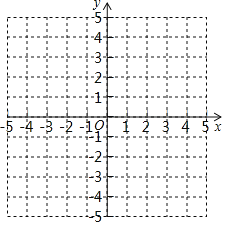
(1)依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
(2)在这个函数图象上有一点P(x,y)(x<0),过点P分别作x轴和y轴的垂线,并延长与直线y=x﹣2交于A、B两点,若△PAB的面积等于![]() ,求出P点坐标.
,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
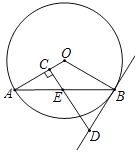
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com