
����Ŀ�������龳
��ͼ 1����ABC �У��ء�BAC ��ƽ���� AB1 �۵��������ص����֣������²����ء�B1A1C ��ƽ���� A1B2 �� ���������ص����֣���˷����������� ��Bn An C ��ƽ���� An Bn��1 �۵����� Bn ��� C �غϣ����Ǿͳ� ��BAC�ǡ�ABC �����ǣ�
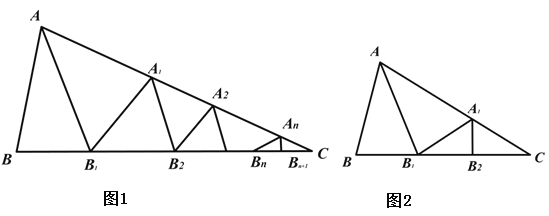
��ͼ 2 Ϊ������ABC �У���B=70�㣬��C=35�㣬���ء�BAC ��ƽ���� AB1 �۵������AA1B=70��.�� A1B1 �����ص����֣������µġ�B1A1C �У��������ε��ڽǺͶ�����֪��A1B1C=35�㣬���ء�B1A1C ��ƽ���� A1B2 �ڶ����۵������ B1 ��� C �غ�. ��ʱ�����Ǿͳơ�BAC �ǡ�ABC ������.
̽������
��1����ABC �У���B= 2��C ���������۵���BAC �Dz��ǡ�ABC �����ǣ� ����ǡ����ǡ� ) .
��2��С�����������۵����֡�BAC �ǡ�ABC �����ǣ��� ��B ���C �������� ��B ����C ) ֮��ĵ�����ϵ Ϊ ��
�����������ݲ��룺������ n ���۵� ��BAC �ǡ�ABC �����ǣ����B �� ��C ���������B�� ��C ) ֮�� �ĵ�����ϵΪ ��
Ӧ������
��3�����һ�������ε���С���� 10�㣬ֱ��д�������������������ǵĶ�����ʹ�ô������ε������Ǿ��� ��������.
���𰸡���1���ǣ���2�� B 3C �� B nC����3��10����160��
��������
��1����ϸ������������۵������ʼ����С����ǡ��Ķ��弴�������жϣ�
��2����Ϊ���������۵���BAC�ǡ�ABC�����ǣ����Ե������۵��ġ�A2 B2C=��C���ɡ�AB B1=��AA1B1����AA1B1=��A1B1C+��C���֡�A1B1C=��A1A2B2����A1A2B2=��A2B2C+��C����ABB1=��A1B1C+��C=��A2B2C+��C+��C=3��C���ɴ˼�����ý����
��3����Ϊ��С����10���ǡ�ABC�����ǣ��������Ƕ��壬����������Ƿֱ�Ϊ10m�㣬10mn�㣨����m��n���������������������10m+10mn+10=180������m��n+1��=17���ٸ���m��n�����������ɵ�m��n+1��17���������ӣ��Ӷ�������ý��.
��1�����ء�BAC��ƽ����AB1�۵���
���B=��AA1B1��
�֡ߡ�AA1B1=��A1B1C+��C�ҡ�B= 2��C
��2��C=��A1B1C+��C����C=��A1B1C
����ƽ����A1B2
���B1 A1 B2 =��C A1 B2
�� B1 A1 B2�� C A1 B2
�ཫ���²����ء�B1A1C��ƽ����A1B2�۵�����ʱ��B1���C�غϣ�
���BAC�Dz��ǡ�ABC������
����ǣ�
��2���۵����������ͼ��

�߸����۵�������֪����B=��AA1B1����A1B1C=��A1A2B2����C=��A2B2C��
���A1A2B2=��C+��A2B2C=2��C��
���AA1B1=��A1B1C+��C=��A1A2B2+��C=2��C+��C=3��C
���B=��AA1B1=3��C������B=3��C
�����B=3��C��
���۵�1��֪������B=��Cʱ����BAC�ǡ�ABC�����ǣ�
���۵�2��֪������B=2��Cʱ����BAC�ǡ�ABC�����ǣ�
���۵�3��֪������B=3��Cʱ����BAC�ǡ�ABC�����ǣ�
��������n���۵���BAC�ǡ�ABC������,���B���C(�������B>��C)֮��ĵ�����ϵΪ��B=n��C
�����B=n��C��
��3���ɡ�B=n��C����BAC�ǡ�ABC�����ǣ�
��Ϊ��С����10���ǡ�ABC�����ǣ�
�������Ƕ���,����������Ƿֱ�Ϊ10m��,10mn��(����m��n����������)��
������,��10m+10mn+10=180,����m(n+1)=,17��
��m��n����������������m��n+1��17���������ӣ�
��m=1��n+1=17��
��m=1��n=16��
��10m=10��,10mn=160����
��������ε����������ǵĶ����ֱ�Ϊ��10����160��.


 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ˮƽ�IJ�����ߣ����Ƕ���������ˮ����Ҫ��ҲԽ��Խ�ߣ�����ľ���ѡ������þ�ˮ����һ�̼�ץס�̻������������ҹ�����![]() ��
��![]() �����ͺż��þ�ˮ������֪����2̨
�����ͺż��þ�ˮ������֪����2̨![]() �ͺż��þ�ˮ����1̨
�ͺż��þ�ˮ����1̨![]() �ͺż��þ�ˮ������200Ԫ������3̨
�ͺż��þ�ˮ������200Ԫ������3̨![]() �ͺž�ˮ����2̨
�ͺž�ˮ����2̨![]() �ͺż��þ�ˮ������6600Ԫ
�ͺż��þ�ˮ������6600Ԫ
��1����![]() ��
��![]() �����ͺż��þ�ˮ��ÿ̨���۸�Ϊ����Ԫ��
�����ͺż��þ�ˮ��ÿ̨���۸�Ϊ����Ԫ��
��2�����̼��ò�����26400Ԫ������![]() ��
��![]() �����ͺż��þ�ˮ��20̨���ٽ������������ͺż��þ�ˮ���ֱ�Ӽ�
�����ͺż��þ�ˮ��20̨���ٽ������������ͺż��þ�ˮ���ֱ�Ӽ�![]() ����ۣ��������ͺż��þ�ˮ��ȫ���۳���ë������12000Ԫ�����̼ҹ���
����ۣ��������ͺż��þ�ˮ��ȫ���۳���ë������12000Ԫ�����̼ҹ���![]() ��
��![]() �����ͺż��þ�ˮ��������̨����ע��ë����
�����ͺż��þ�ˮ��������̨����ע��ë����![]() �ۼ�
�ۼ�![]() ���ۣ�
���ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���֪��D��E��F�ֱ�ΪBC��AD��AE���е㣬��S��ABC=4cm2������Ӱ�������S=��������cm2��
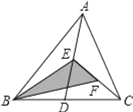
A. 1B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
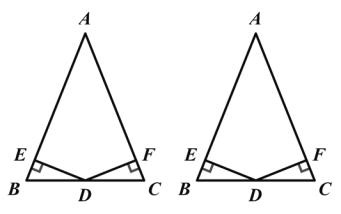
����Ŀ����֪:��ͼ���ڡ�ABC �У�AB=AC���� D �� BC �ϣ�DE��AB��DF��AC������ֱ�Ϊ�� E��F,�� DE=DF.
��֤���� D Ϊ BC ���е�.���������ֲ�ͬ�ķ���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019 �� 4 �� 27 �գ��ڶ��조һ��һ·�����ʺ����߷���̳Բ����Ļ����һ��һ·���ѳ�Ϊ�ҹ�����ȫ�ź���������ȫ��������ϵ���ٽ�ȫ��ͬ��չ���١��ƶ������������˹�ͬ����й�������������ŷ���м�֤�ˡ�һ��һ·��������ͨ�Ŀ�Խʽ��չ�������ͻ�����ֵ�� 2011 ��IJ��� 6 ����Ԫ����չ�� 2018 ���Լ 160 ����Ԫ�������� 2011-2018 ����ŷ���п����������������ʵ�ͳ��ͼ��
����ͼ���ṩ����Ϣ��գ�
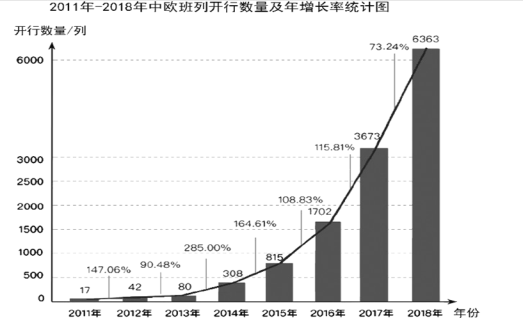
��1��2018 �꣬��ŷ���п�����������������_____��
��2����� 2019 ����ŷ���еĿ������������ʲ����� 50%����ô 2019 ����ŷ���п�������������_____�У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B����C��AD��BC������ΪD��AEƽ����BAC����֪��B=65������DAE=20��������C�Ķ�����
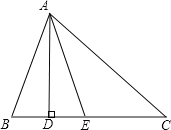
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ�� P ���߶� a�������� P ���߶� a ����ֱ�������ߣ������������߶� a �ϣ���Ƶ� P Ϊ�߶�a ���ڴ��㣮��ƽ��ֱ������ϵ xOy �У���֪�� A(-1��0)��B(2��0 ) ��C(0��2)��
��1���ڵ� M��1��0����N��3��2����P��-1��-3���У����߶� AB ���ڴ������ ��
��2����֪�� D��-3��2����E��-3��4������ͼ�л�����������Ӱ��ʾ��ʹ�����ڵ�ÿ�����Ϊ Rt��CDE���ߵ��ڴ��㣻
��3����ֱ֪�� m �� x �ύ�ڵ� B���� y �ύ�ڵ� C����ֱ�� m �� y ��ƽ�� 3 ����λ���ȵõ�ֱ�� n �� �����ڵ� Q��ʹ�߶� BQ ���ڴ����γɵ�����ǡ����ֱ�� m �� n ֮����������߽磩��ֱ��д���� Q �����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ���������������߶�AB��CD��EF��GH���߶ζ˵��ڸ���ϣ���
��ѡȡ���������߶Σ�ʹ���������߶���Χ��һ��ֱ�������Σ�
��ѡȡ�������߶�Ϊ ��
��ֻ�䶯���������߶ε�λ�ã���ԭͼ�л���һ�����������ֱ�������Σ��������ڸ�㣬�����ϱ�Ҫ����ĸ����
�𣺻�����ֱ��������Ϊ�� ��
������ֱ�������ε����Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���������OABC�Ƶ�O��ʱ����ת45����õ�������OA1B1C1�����˷�ʽ���Ƶ�O������ת2018�εõ�������OA2018B2018C2018�������A������Ϊ��1��0������ô��B2018������Ϊ��������
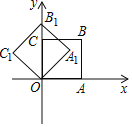
A. ��1��1�� B. ��0��![]() �� C. ��
�� C. ��![]() �� D. ����1��1��
�� D. ����1��1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com