
����Ŀ��2019 �� 4 �� 27 �գ��ڶ��조һ��һ·�����ʺ����߷���̳Բ����Ļ����һ��һ·���ѳ�Ϊ�ҹ�����ȫ�ź���������ȫ��������ϵ���ٽ�ȫ��ͬ��չ���١��ƶ������������˹�ͬ����й�������������ŷ���м�֤�ˡ�һ��һ·��������ͨ�Ŀ�Խʽ��չ�������ͻ�����ֵ�� 2011 ��IJ��� 6 ����Ԫ����չ�� 2018 ���Լ 160 ����Ԫ�������� 2011-2018 ����ŷ���п����������������ʵ�ͳ��ͼ��
����ͼ���ṩ����Ϣ��գ�
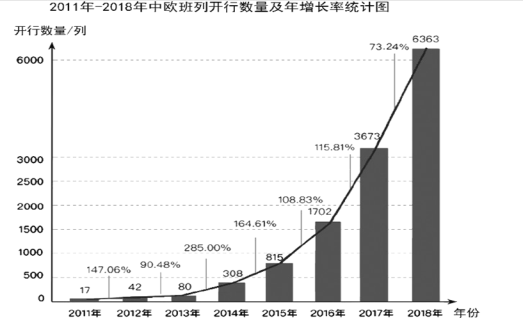
��1��2018 �꣬��ŷ���п�����������������_____��
��2����� 2019 ����ŷ���еĿ������������ʲ����� 50%����ô 2019 ����ŷ���п�������������_____�У�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��AB�Ĵ�ֱƽ����MN��AC�ڵ�D����AB�ڵ�E��
��1������A��40�㣬���DBC�Ķ�����
��2����AE��6����CBD���ܳ�Ϊ20����BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�У��߳�Ϊ10���ף���E��AB���ϣ�BE=6���ף������P���߶�BC����4����/����ٶ���B����C���˶���ͬʱ����Q���߶�CD����C����D���˶���
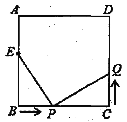
��1������Q���˶��ٶ����P���˶��ٶ���ȣ����� ���BPE�ա�CQP��
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPE���CQPȫ�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���۲���κ���y=ax2+bx+c��ͼ�����н��ۣ�
��a+b+c��0����2a+b��0����b2��4ac��0����ac��0��
������ȷ���ǣ� ��
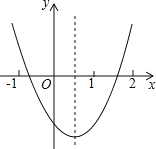
A���٢� B���٢� C���ڢ� D���ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����Ϊ����3����6����������y=ax2+bx+c�����㣨��1����4���������н����д�����ǣ�������

A. b2��4ac
B. ax2+bx+c�ݩ�6
C. ���㣨��2��m��������5��n�����������ϣ���m��n
D. ����x��һԪ���η���ax2+bx+c=��4������Ϊ��5�ͩ�1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳
��ͼ 1����ABC �У��ء�BAC ��ƽ���� AB1 �۵��������ص����֣������²����ء�B1A1C ��ƽ���� A1B2 �� ���������ص����֣���˷����������� ��Bn An C ��ƽ���� An Bn��1 �۵����� Bn ��� C �غϣ����Ǿͳ� ��BAC�ǡ�ABC �����ǣ�
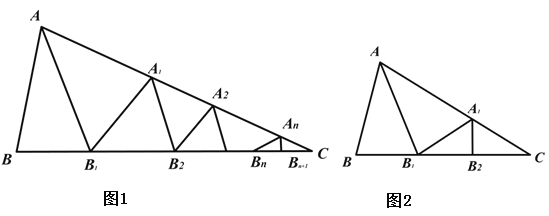
��ͼ 2 Ϊ������ABC �У���B=70�㣬��C=35�㣬���ء�BAC ��ƽ���� AB1 �۵������AA1B=70��.�� A1B1 �����ص����֣������µġ�B1A1C �У��������ε��ڽǺͶ�����֪��A1B1C=35�㣬���ء�B1A1C ��ƽ���� A1B2 �ڶ����۵������ B1 ��� C �غ�. ��ʱ�����Ǿͳơ�BAC �ǡ�ABC ������.
̽������
��1����ABC �У���B= 2��C ���������۵���BAC �Dz��ǡ�ABC �����ǣ� ����ǡ����ǡ� ) .
��2��С�����������۵����֡�BAC �ǡ�ABC �����ǣ��� ��B ���C �������� ��B ����C ) ֮��ĵ�����ϵ Ϊ ��
�����������ݲ��룺������ n ���۵� ��BAC �ǡ�ABC �����ǣ����B �� ��C ���������B�� ��C ) ֮�� �ĵ�����ϵΪ ��
Ӧ������
��3�����һ�������ε���С���� 10�㣬ֱ��д�������������������ǵĶ�����ʹ�ô������ε������Ǿ��� ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������˽����ׯ 130 ����ͥ�ľ�����������������ȡ�˲��ּ�ͥ���е��飬��������ǵ������루��λ����Ԫ�����������ݣ������룩���������������ͷ�������������˲�����Ϣ��
a������ȡ�IJ��ּ�ͥ�������Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ���£����ݷ��飺0.9��x��1.3��1.3��x��1.7 �� 1.7��x��2.1�� 2.1��x��2.5�� 2.5��x��2.9 �� 2.9��x��3.3 ��
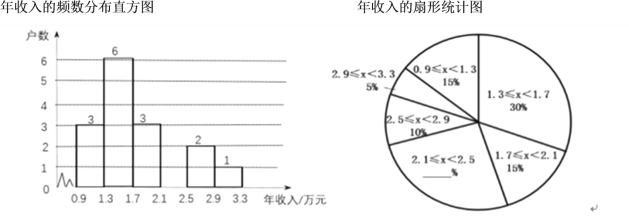
b����ͥ��������1.3��x��1.7 ��һ����ǣ� 1.3 1.3 1.4 1.5 1.6 1.6
����������Ϣ������������⣺
��1��������ͳ��ͼ����������
��2���������ׯ�ж��ٻ���ͥ�����벻���� 1.5 ��Ԫ�Ҳ��� 2.1 ��Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��AOB��60����OC�ǡ�AOB��ƽ���ߣ���DΪOC��һ�㣬��D��ֱ��DE��OA������Ϊ��E����ֱ��DE��OB�ڵ�F����ͼ��ʾ����DE��2����DF��_____��
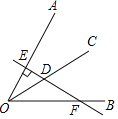
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BC��AC��Բ��O��AC�ϣ���M���C�ֱ���AC����O�Ľ��㣬��D��MB����O�Ľ��㣬��P��AD�ӳ�����BC�Ľ��㣬��![]() ��
��
��1����֤��PD����O�����ߣ�
��2����AD=12��AM=MC����![]() ��ֵ��
��ֵ��
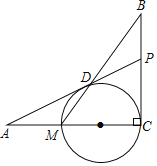
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com