
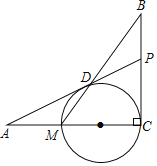
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且![]() .
.
(1)求证:PD是⊙O的切线;
(2)若AD=12,AM=MC,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】(1)欲证明PD是⊙O的切线,只要证明OD⊥PA即可解决问题;
(2)连接CD.由(1)可知:PC=PD,由AM=MC,推出AM=2MO=2R,在Rt△AOD中,OD2+AD2=OA2,可得R2+122=9R2,推出R=3![]() ,推出OD=3
,推出OD=3![]() ,MC=6
,MC=6![]() ,由
,由![]() ,可得DP=6,再利用相似三角形的性质求出MD即可解决问题.
,可得DP=6,再利用相似三角形的性质求出MD即可解决问题.
(1)如图,连接OD、OP、CD,
∵![]() ,∠A=∠A,
,∠A=∠A,
∴△ADM∽△APO,
∴∠ADM=∠APO,
∴MD∥PO,
∴∠1=∠4,∠2=∠3,
∵OD=OM,
∴∠3=∠4,
∴∠1=∠2,
∵OP=OP,OD=OC,
∴△ODP≌△OCP,
∴∠ODP=∠OCP,
∵BC⊥AC,
∴∠OCP=90°,
∴OD⊥AP,
∴PD是⊙O的切线;
(2)如图,连接CD,由(1)可知:PC=PD,
∵AM=MC,
∴AM=2MO=2R,
在Rt△AOD中,OD2+AD2=OA2,
∴R2+122=9R2,
∴R=3![]() ,
,
∴OD=3![]() ,MC=6
,MC=6![]() ,
,
∵![]() ,
,
∴DP=6,
∵O是MC的中点,
∴![]() ,
,
∴点P是BC的中点,
∴BP=CP=DP=6,
∵MC是⊙O的直径,
∴∠BDC=∠CDM=90°,
在Rt△BCM中,∵BC=2DP=12,MC=6![]() ,
,
∴BM=6![]() ,
,
∵△BCM∽△CDM,
∴![]() ,即
,即![]() ,
,
∴MD=2![]() ,
,
∴![]() .
.



 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】2019 年 4 月 27 日,第二届“一带一路”国际合作高峰论坛圆满闭幕.“一带一路”已成为我国参与全球开放合作、改善全球经济治理体系、促进全球共同发展繁荣、推动构建人类命运共同体的中国方案.其中中欧班列见证了“一带一路”互联互通的跨越式发展,年运送货物总值由 2011 年的不足 6 亿美元,发展到 2018 年的约 160 亿美元.下面是 2011-2018 年中欧班列开行数量及年增长率的统计图.
根据图中提供的信息填空:
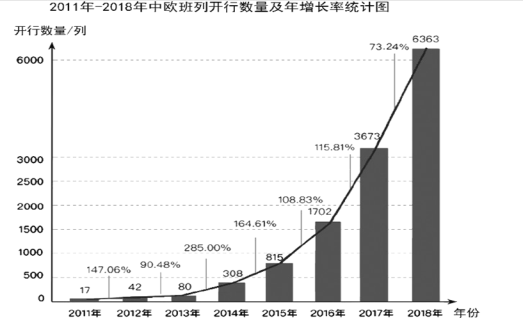
(1)2018 年,中欧班列开行数量的增长率是_____;
(2)如果 2019 年中欧班列的开行数量增长率不低于 50%,那么 2019 年中欧班列开行数量至少是_____列.
查看答案和解析>>
科目:初中数学 来源: 题型:
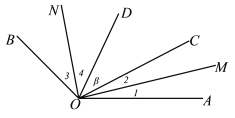
【题目】如图,射线OC、OD在∠AOB内部,∠AOB=![]() ,∠COD=
,∠COD=![]() ,分别作∠AOC和∠BOD的平分线OM、ON,
,分别作∠AOC和∠BOD的平分线OM、ON,
(1)当![]() =130°,
=130°,![]() =40°时,请你填空:∠1+∠3=______°,∠MON=______°;
=40°时,请你填空:∠1+∠3=______°,∠MON=______°;
(2)聪明的小芳通过探究发现,当射线OC、OD的位置在∠AOB内变化时,∠MON与![]() 、
、![]() 之间总满足∠MON=
之间总满足∠MON=![]() ,你是否认同她的这一结论?请说明理由;
,你是否认同她的这一结论?请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:![]() ···①,
···①,![]() ···②,
···②,![]() …③,…
…③,…
探索以上式子的规律.
(1)第7个式子是_______;
(2)试写出第![]() 个等式,并说明第
个等式,并说明第![]() 个等式成立;
个等式成立;
(3)根据以上规律写出第2019个式子:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
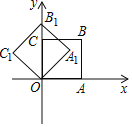
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD为∠ABC的平分线,DE⊥BC于E,且AB+BC=2BE.
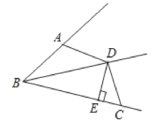
(1)求证:∠BAD+∠BCD=180°;
(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换,结论还成立吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com