
【题目】观察下列各式:![]() ···①,
···①,![]() ···②,
···②,![]() …③,…
…③,…
探索以上式子的规律.
(1)第7个式子是_______;
(2)试写出第![]() 个等式,并说明第
个等式,并说明第![]() 个等式成立;
个等式成立;
(3)根据以上规律写出第2019个式子:______.
【答案】(1)13×17+4=152;(2)(2n-1)(2n+3)+4=(2n+1)2,理由见解析;(3)4037×4041+4=40392
【解析】
(1)根据题意题意列出式子即可;
(2)根据以上所的规律列出等式即可得,再利用整式的混合运算验证左右两边是否相等即可.
(3)根据规律进行计算即可解答;
(1)第7个等式为13×17+4=152;
(2)由题意知(2n-1)(2n+3)+4=(2n+1)2,
理由:左边=4n2+6n-2n-3+4=4n2+4n+1=(2n+1)2=右边,
∴(2n-1)(2n+3)+4=(2n+1)2.
(3)(2n-1)(2n+3)+4=(2n+1)2
n=2019,得到:(2×2019-1)(2×2019+3)+4=(2×2019+1)2
故答案为:4037×4041+4=40392


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,观察二次函数y=ax2+bx+c的图象,下列结论:
①a+b+c>0,②2a+b>0,③b2﹣4ac>0,④ac>0.
其中正确的是( )
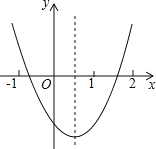
A.①② B.①④ C.②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=_____.
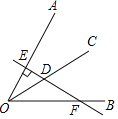
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知变量x、y对应关系如下表已知值呈现的对应规律.
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | 4 | … |
y | … |
|
| 1 | 2 | ﹣2 | ﹣1 | ﹣ | ﹣ | … |
(1)依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
(2)在这个函数图象上有一点P(x,y)(x<0),过点P分别作x轴和y轴的垂线,并延长与直线y=x﹣2交于A、B两点,若△PAB的面积等于![]() ,求出P点坐标.
,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且![]() .
.
(1)求证:PD是⊙O的切线;
(2)若AD=12,AM=MC,求![]() 的值.
的值.
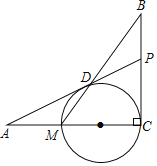
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级的同学参加了一项“节能环保”的社会调查活动,为了了解家庭用电的情况,他们随机调查了某城区50 个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).

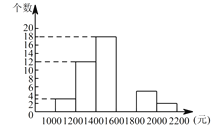
请你根据以上提供的信息,解答下列问题:
(1)频数分布表中 ![]() ________________,
________________,![]() ________________,
________________,
(2)补全频数分布直方图;
(3)这 ![]() 个家庭电费支出的中位数落在________组内;
个家庭电费支出的中位数落在________组内;
(4)若该城区有 ![]() 万个家庭,请你估计该城区有多少个一年电费支出低于
万个家庭,请你估计该城区有多少个一年电费支出低于 ![]() 元的家庭?
元的家庭?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com