
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
【答案】(1)m的值为6;(2)17.
【解析】试题分析:
(1)由题意和根与系数的关系可得:x1+x2=2(m+1),x1x2=m2+5;由(x1-1)(x2-1)=28,可得:x1x2-(x1+x2)=27;从而得到:m2+5-2(m+1)=27,解方程求得m的值,再由“一元二次方程根的判别式”进行检验即可得到m的值;
(2)①当7为腰长时,则方程的两根中有一根为7,代入方程可解得m的值(此时m的取值需满足根的判别式△![]() ),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
),将m的值代入原方程,可求得两根(此时两根和7需满足三角形三边之间的关系),从而可求得等腰三角形的周长;
②当7为底边时,则方程的两根相等,由此可得“根的判别式△=0”,从而可得关于m的方程,解方程求得m的值,代入原方程可求得方程的两根,再由三角形三边之间的关系检验即可.
试题解析:
(1)(x1-1)(x2-1)=28,即x1x2-(x1+x2)=27,而x1+x2=2(m+1),x1x2=m2+5,
∴m2+5-2(m+1)=27,
解得m1=6,m2=-4,
又Δ=[-2(m+1)]2-4×1×(m2+5)≥0时,m≥2,
∴m的值为6;
(2) 若7为腰长,则方程x2-2(m+1)x+m2+5=0的一根为7,
即72-2×7×(m+1)+m2+5=0,
解得m1=10,m2=4,
当m=10时,方程x2-22x+105=0,根为x1=15,x2=7,不符合题意,舍去.
当m=4时,方程为x2-10x+21=0,根为x1=3,x2=7,此时周长为7+7+3=17
若7为底边,则方程x2-2(m+1)x+m2+5=0有两等根,
∴Δ=0,解得m=2,此时方程为x2-6x+9=0,根为x1=3,x2=3,3+3<7,不成立,
综上所述,三角形周长为17


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )

A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论:①AD是∠BAC的平分线;②若∠B=30°,则DA=DB;③AB:AC=2:1;④点D在AB的垂直平分线上.一定成立的个数为( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论:①AD是∠BAC的平分线;②若∠B=30°,则DA=DB;③AB:AC=2:1;④点D在AB的垂直平分线上.一定成立的个数为( )
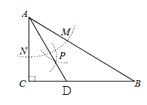
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F为BC中点,连接AE.
(1)直接写出∠BAE的度数为 ;
(2)判断AF与CE的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明:小强想证明下面的问题:“有两个角(图中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的
)相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的![]() 和边
和边![]() .
.
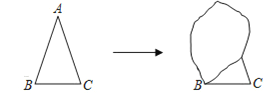
(1)请问:他能够把图恢复成原来的样子吗?若能,请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子.

(2)你能够证明这样的三角形是等腰三角形吗?(至少用两种方法证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是( )
A.抛物线开口向上
B.抛物线的对称轴是x=1
C.当x=1时,y的最大值为-4
D.抛物线与x轴的交点为(-1,0),(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。
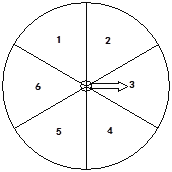
其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com