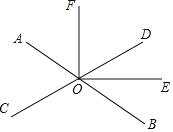
【题目】如图，直线AB、CD相交于点O，OE平分∠BOD
（1）若∠AOC＝60°，求∠BOE的度数；
（2）若OF平分∠AOD，试说明OE⊥OF．
阳光课堂课时优化作业系列答案科目：初中数学 来源： 题型：
【题目】阅读下列解题过程
例：若代数式
的值是
，求
的取值范围．
解：原式=
当
时，原式
，解得
(舍去)；
当
时，原式
，符合条件；
当
时，原式
，解得 
(舍去)．
所以，的取值范围是
上述解题过程主要运用了分类讨论的方法，请你根据上述理解，解答下列问题：
当
时，化简：
若等式
成立，则的取值范围是
若
，求的取值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC 中，AD 是 BC 边上的高，且∠ACB＝∠BAD，AE 平分∠CAD，交 BC于点 E，过点 E 作 EF∥AC，分别交 AB、AD 于点 F、G．则下列结论：①∠BAC＝90°；②∠AEF＝∠BEF； ③∠BAE＝∠BEA； ④∠B＝2∠AEF，其中正确的有（ ）
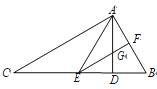
A. 4 个B. 3 个C. 2 个D. 1 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】花香村计划改造一片林地，估计这片林地可种梨树80~133棵.根据经验，若种100棵树，果树成熟后平均每棵树上能结500个梨，在这个基础上每多种一棵梨树，平均每棵会少结3个梨，每少种一棵，平均每棵树会多结4个梨.
（1）如果种植110棵梨树，则总共能结多少个梨？
（2）设种植x棵梨树，总共能结y个梨，
①当80≤x≤100时，求出y与x之间的函数关系式；
②当100<x≤134时，求出y与x之间的函数关系式；
（3）种多少棵梨树，总共能结的梨数最多？最多是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场销售同型号A、B两种品牌节能灯管，它们进价相同，A品牌售价可变，最低售价不能低于进价，最高利润不超过4元，B品牌售价不变．它们的每只销售利润与每周销售量如下表：（售价=进价+利润）
（1）当A品牌每周销售量为300只时，B品牌每周销售多少只？
（2）A品牌节能灯管每只利润定为多少元时？可获得最大总利润，并求最大总利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读下面的解题过程，再解答问题：
如图①，已知AB∥CD，∠B＝40°，∠D＝30°，求∠BED的度数．
解：过点E作EF∥AB，则AB∥CD∥EF，
因为EF∥AB，所以∠1＝∠B＝40°
又因为CD∥EF，所以∠2＝∠D＝30°
所以∠BED＝∠1+∠2＝40°+30°＝70°．
如图②是小军设计的智力拼图玩具的一部分，现在小军遇到两个问题，请你帮他解决：
（1）如图②∠B＝45°，∠BED＝75°，为了保证AB∥CD，∠D必须是多少度？请写出理由．
（2）如图②，当∠G、∠GFP、∠P满足什么关系时，GH∥PQ，请直接写出满足关系的式子，并在如图②中画出需要添加的辅助线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解方程：(1) 
； （2）
.
【答案】（1）x1 =1 ，x2=
； (2) x1 =-1，x2=
.
【解析】试题分析：
根据两方程的特点，使用“因式分解法”解两方程即可.
试题解析：
（1）原方程可化为： 
，
方程左边分解因式得： 
，
或
，
解得： 
， 
.
（2）原方程可化为： 
，即
，
∴
，
∴
或
，
解得： 
.
【题型】解答题
【结束】
20
【题目】已知x1，x2是关于x的一元二次方程x2－2(m＋1)x＋m2＋5＝0的两实根．
(1)若(x1－1)(x2－1)＝28，求m的值；
(2)已知等腰△ABC的一边长为7，若x1，x2恰好是△ABC另外两边的边长，求这个三角形的周长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
