
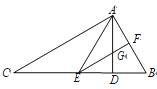
【题目】如图,在△ABC 中,AD 是 BC 边上的高,且∠ACB=∠BAD,AE 平分∠CAD,交 BC于点 E,过点 E 作 EF∥AC,分别交 AB、AD 于点 F、G.则下列结论:①∠BAC=90°;②∠AEF=∠BEF; ③∠BAE=∠BEA; ④∠B=2∠AEF,其中正确的有( )
A. 4 个B. 3 个C. 2 个D. 1 个
【答案】B
【解析】
利用高线和同角的余角相等,三角形内角和定理即可证明①,再利用等量代换即可得到③
④均是正确的,②缺少条件无法证明.
解:由已知可知∠ADC=∠ADB=90°,
∵∠ACB=∠BAD
∴90°-∠ACB=90°-∠BAD,即∠CAD=∠B,
∵三角形ABC的内角和=∠ACB+∠B+∠BAD+∠CAD=180°,
∴∠CAB=90°,①正确,
∵AE平分∠CAD,EF∥AC,
∴∠CAE=∠EAD=∠AEF,∠C=∠FEB=∠BAD,②错误,
∵∠BAE=∠BAD+∠DAE,∠BEA=∠BEF+∠AEF,
∴∠BAE=∠BEA,③正确,
∵∠B=∠DAC=2∠CAE=2∠AEF,④正确,
综上正确的一共有3个,故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的长度.她先在山脚下点E处测得山顶A的仰角是30°,然后,她沿着坡度是i=1:1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度.(参考数据: ![]() ≈1.41,结果精确到0.1米)
≈1.41,结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A.
求作:l的平行线,使它经过点A.

小云的作法如下:
(1)在直线l上任取一点B;
(2)以B为圆心,BA长为半径作弧,交直线l于点C;
(3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D;
(4)作直线AD.直线AD即为所求.

小云作图的依据是_______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱![]() 台,这100台家电的销售总利润为
台,这100台家电的销售总利润为![]() 元,要求购进空调数量不超过电冰箱数量的2倍,试确定获利最大的方案以及最大利润.
元,要求购进空调数量不超过电冰箱数量的2倍,试确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张强在一次投掷铅球时,刚出手时铅球离地面![]() m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
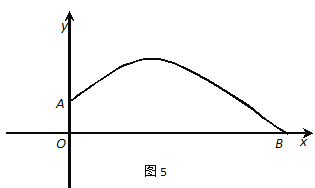
(1)请确定这个抛物线的顶点坐标
(2)求抛物线的函数关系式
(3)张强这次投掷成绩大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
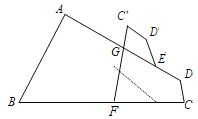
【题目】如图,在四边形 ABCD 中,∠C+∠D=210°,E、F 分别是 AD,BC 上的点,将四边形 CDEF 沿直线 EF 翻折,得到四边形 C′D′EF, C′F 交 AD 于点 G,若△EFG 有两个角相等,则∠EFG=______ °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在BC上,DE∥AC,DF∥AB,下列四个判断中不正确的是( )

A.四边形AEDF是平行四边形
B.若∠BAC=90°,则四边形AEDF是矩形
C.若AD平分∠BAC,则四边形AEDF是矩形
D.若AD⊥BC且AB=AC,则四边形AEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com