
【题目】花香村计划改造一片林地,估计这片林地可种梨树80~133棵.根据经验,若种100棵树,果树成熟后平均每棵树上能结500个梨,在这个基础上每多种一棵梨树,平均每棵会少结3个梨,每少种一棵,平均每棵树会多结4个梨.
(1)如果种植110棵梨树,则总共能结多少个梨?
(2)设种植x棵梨树,总共能结y个梨,
①当80≤x≤100时,求出y与x之间的函数关系式;
②当100<x≤134时,求出y与x之间的函数关系式;
(3)种多少棵梨树,总共能结的梨数最多?最多是多少?
【答案】(1)51700(2)①![]() ②
②![]() (3)当x=133时,有最大值,最大值是53333个梨
(3)当x=133时,有最大值,最大值是53333个梨
【解析】试题分析:(1)、根据题意首先得出每棵树上能结多少果实,然后求出总量;(2)、当80≤x≤100时,平均每棵树上能结[500+4(100-x)]个梨,然后得出函数解析式;当100<x≤120时,平均每棵树上能结[500-3(x-100)]个梨,然后得出函数解析式;(3)、根据两个函数解析式,分别求出每个区间范围内的最大值,最后选择更加大的值得出答案.
试题解析:(1)、如果种110棵树,平均每棵树上能结(500-30)个梨,则总共结51700个梨.
(2)、①、设种植x棵梨树(80≤x≤100),则平均每棵树上能结[500+4(100-x)]个梨,
∴![]() ;
;
②、设种植x棵梨树(100<x≤120),则平均每棵树上能结[500-3(x-100)]个梨,
∴![]() ;
;
(3)、当80≤x≤100时,由于对称轴x=![]() ,所以y随x的增大而增大,
,所以y随x的增大而增大,
故当x=100时,y有最大值,最大值是50000个;
当100<x≤133,![]()
所以当x=133时,有最大值,最大值是53333个梨;
综上所述:当x=133时,有最大值,最大值是53333个梨.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,研究发现了此类方程的一般性结论:设其中一根为![]() ,则另一个根为
,则另一个根为![]() ,因此
,因此![]() ,所以有
,所以有![]() ;我们记“
;我们记“![]() ”即
”即![]() 时,方程
时,方程![]() 为倍根方程;
为倍根方程;
下面我们根据此结论来解决问题:
(1)方程①![]() ;方程②
;方程②![]() ;方程③
;方程③![]() 这几个方程中,是倍根方程的是_________(填序号即可);
这几个方程中,是倍根方程的是_________(填序号即可);
(2)若![]() 是倍根方程,则
是倍根方程,则![]() 的值为______;
的值为______;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张强在一次投掷铅球时,刚出手时铅球离地面![]() m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图5所示:
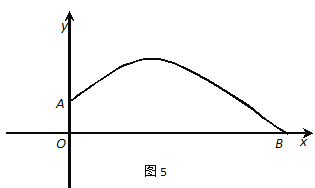
(1)请确定这个抛物线的顶点坐标
(2)求抛物线的函数关系式
(3)张强这次投掷成绩大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形 ABCD 中,∠C+∠D=210°,E、F 分别是 AD,BC 上的点,将四边形 CDEF 沿直线 EF 翻折,得到四边形 C′D′EF, C′F 交 AD 于点 G,若△EFG 有两个角相等,则∠EFG=______ °.
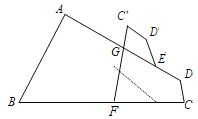
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和格点P.
(1)以A点为位似中心,将△ABC在网格中放大成△AB1C1,使![]() =2,请画出△AB1C1;
=2,请画出△AB1C1;
(2)以P点为三角形的一个顶点,请画一个格点△PMN,使△PMN∽△ABC,且相似比为![]() .
.
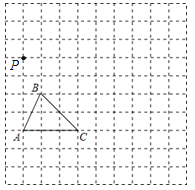
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论:①AD是∠BAC的平分线;②若∠B=30°,则DA=DB;③AB:AC=2:1;④点D在AB的垂直平分线上.一定成立的个数为( )
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列结论:①AD是∠BAC的平分线;②若∠B=30°,则DA=DB;③AB:AC=2:1;④点D在AB的垂直平分线上.一定成立的个数为( )
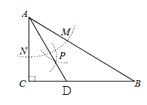
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com