
【题目】如图,△ABC是等边三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F为BC中点,连接AE.
(1)直接写出∠BAE的度数为 ;
(2)判断AF与CE的位置关系,并说明理由.

【答案】(1)90°;(2)AF∥EC,见解析
【解析】
(1)分别利用等边三角形的性质和等腰三角形的性质求出∠BAC,∠CAE的度数,然后利用∠BAE=∠BAC+∠CAE即可解决问题;
(2)根据等边三角形的性质有AF⊥BC,然后利用等边三角形的性质和等腰三角形的性质得出,∠BCE=90°则有EC⊥BC,再根据垂直于同一条直线的两直线平行即可得出结论.
解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∵EA=EC,∠AEC=120°,
∴EAC=∠ECA=30°,
∴∠BAE=∠BAC+∠CAE=90°.
故答案为90°.
(2)结论:AF∥EC.
理由:∵AB=AC,BF=CF,
∴AF⊥BC,
∵∠ACB=60°,∠ACE=30°,
∴∠BCE=90°,
∴EC⊥BC,
∴AF∥EC.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图像相交于点
的图像相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)填空:![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
(2)观察反比函数![]() 的图像,当
的图像,当![]() 时,请直接写出自变量
时,请直接写出自变量![]() 的取值范围;
的取值范围;
(3)以![]() 为边作菱形
为边作菱形![]() ,使点
,使点![]() 在
在![]() 轴负半轴上,点
轴负半轴上,点![]() 在第二象限内,求点
在第二象限内,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300 m2.若设道路宽为x m,根据题意可列出方程为______________________________.
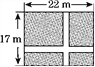
【答案】(22-x)(17-x)=300(或x2-39x+74=0)
【解析】试题分析:把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程.设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,故答案为:(22﹣x)(17﹣x)=300.
考点:由实际问题抽象出一元二次方程.
【题型】填空题
【结束】
17
【题目】x=1是关于x的一元二次方程x2+mx﹣5=0的一个根,则此方程的另一个根是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D,旋转角为![]() .
.
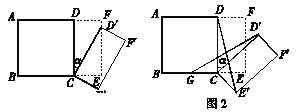
(1)当点D′恰好落在EF边上时,则旋转角α的值为________度;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,是否存在旋转角α,使△DCD′与△CBD′全等?若能,直接写出旋转角α的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 的坐标为
的坐标为![]() ,将点
,将点![]() 向右平移
向右平移![]() 个单位得到点
个单位得到点![]() ,其中关于
,其中关于![]() 的一元一次不等式
的一元一次不等式![]() 的解集为
的解集为![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() .
.
(1)求![]() 两点坐标及四边形
两点坐标及四边形![]() 的面积;
的面积;
(2)如图2,点![]() 自
自![]() 点以1个单位/秒的速度在
点以1个单位/秒的速度在![]() 轴上向上运动,点
轴上向上运动,点![]() 自
自![]() 点以2个单位/秒的速度在
点以2个单位/秒的速度在![]() 轴上向左运动,设运动时间为
轴上向左运动,设运动时间为![]() 秒(
秒(![]() ),是否存在一段时间使得
),是否存在一段时间使得![]() ,若存在,求出
,若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)在(2)的条件下,求四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应的任务;全等四边形根据全等图形的定又可知:四条边分别相等、四个角也分别相等的两个四边形全等。在“探索三角形全等的条件”时,我们把两个三角形中“一条边和等”或“一个角相等”称为一个条件.智慧小组的同学类比“探索三角形全等条件”的方法探索“四边形全等的条件”,进行了如下思考:如图1,四边形![]() 和四边形
和四边形![]() 中,连接对角线
中,连接对角线![]() ,这样两个四边形全等的问题就转化为“
,这样两个四边形全等的问题就转化为“![]() ”与“
”与“![]() ”的问题。若先给定“
”的问题。若先给定“![]() ”的条件,只要再增加
”的条件,只要再增加![]() 个条件使“
个条件使“![]() ”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。
”即可推出两个四边形中“四条边分别相等、四个角也分别和等”,从而说明两个四边形全等。
按照智慧小组的思路,小明对图![]() 中的四边形
中的四边形![]() 与四边形
与四边形![]() 先给出和下条件:
先给出和下条件: ![]() ,
,![]() ,小亮在此基础上又给出“
,小亮在此基础上又给出“![]() ”两个条件.他们认为满足这五个条件能得到“四边形
”两个条件.他们认为满足这五个条件能得到“四边形![]() 四边形
四边形![]() ”.
”.

(1)请根据小明和小亮给出的条件,说明“四边形![]() 四边形
四边形![]() ”的理由;
”的理由;
(2)请从下面![]() 两题中任选一题作答,我选择 题.
两题中任选一题作答,我选择 题.
![]() 在材料中“小明所给条件”的基础上,小颖又给出两个条件“
在材料中“小明所给条件”的基础上,小颖又给出两个条件“![]() ”.满足这五个条件 (填“能”或“不能”)得到四边形
”.满足这五个条件 (填“能”或“不能”)得到四边形![]() 四边形
四边形![]()
![]() 在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形
在材料中“小明所给条件的基础上”,再添加两个关于原四边形的条件(要求:不同于小亮的条件),使四边形![]() 四边形
四边形![]() ,你添加的条件是① ,② .
,你添加的条件是① ,② .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com