
【题目】(12分)如图1所示,将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至CE′F′D,旋转角为![]() .
.
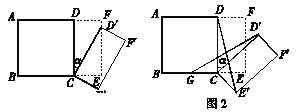
(1)当点D′恰好落在EF边上时,则旋转角α的值为________度;
(2)如图2,G为BC中点,且0°<α<90°,求证:GD′=E′D;
(3)小长方形CEFD绕点C顺时针旋转一周的过程中,是否存在旋转角α,使△DCD′与△CBD′全等?若能,直接写出旋转角α的值;若不能,说明理由.
【答案】(1)30;(2)证明见试题解析;(3)能.![]() 或
或![]() .
.
【解析】
试题分析:(1)根据旋转的性质得到CD′的长,在Rt△CED′中,CD′=2,CE=1,得到∠CD′E=30°,然后根据平行线的性质即可得到∠α的度数;
(2)由G为BC中点可得CG=CE,再根据旋转的性质得∠D′CE′=∠DCE=90°,CE=CE′=CG,则∠GCD′=∠DCE′=90°+α,再根据“SAS”可判断△GCD′≌△E′CD,得到GD′=E′D;
(3)根据正方形的性质得CB=CD,而CD=CD′,则△BCD′与△DCD′为腰相等的两等腰三角形,当两顶角相等时它们全等,当△BCD′与△DCD′为钝角三角形时,可计算出α=135°,当△BCD′与△DCD′为锐角三角形时,可计算得到α=315°.
试题解析:(1)∵长方形CEFD绕点C顺时针旋转至CE′F′D′,∴CD′=CD=2,在Rt△CED′中,CD′=2,CE=1,∴∠CD′E=30°,∵CD∥EF,∴∠α=30°;
(2)∵G为BC中点,∴CG=1,∴CG=CE,∵长方形CEFD绕点C顺时针旋转至CE′F′D′,∴∠D′CE′=∠DCE=90°,CE=CE′=CG,∴∠GCD′=∠DCE′=90°+α,在△GCD′和△E′CD中,∵CD′=CD,∠GCD′=∠DCE′,CG=CE′,∴△GCD′≌△E′CD(SAS),∴GD′=E′D;
(3)能.理由如下:∵四边形ABCD为正方形,∴CB=CD,∵CD′=CD′,∴△BCD′与△DCD′为腰相等的两等腰三角形,当∠BCD′=∠DCD′时,△BCD′≌△DCD′,当△BCD′与△DCD′为钝角三角形时,则旋转角α=![]() =135°,
=135°,
当△BCD′与△DCD′为锐角三角形时,∠BCD′=∠DCD′=![]() ∠BCD=45°,则α=360°﹣
∠BCD=45°,则α=360°﹣![]() =315°,即旋转角a的值为135°或315°时,△BCD′与△DCD′全等.
=315°,即旋转角a的值为135°或315°时,△BCD′与△DCD′全等.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,历来有吃“粽子”的习俗.我市某食品加工厂,拥有A、B两条粽子加工生产线.原计划A生产线每小时加工粽子个数是B生产线每小时加工粽子个数的![]() .
.
(1)若A生产线加工4000个粽子所用时间与B生产线加工4000个粽子所用时间之和恰好为18小时,则原计划A、B生产线每小时加工粽子各是多少个?
(2)在(1)的条件下,原计划A、B生产线每天均加工a小时,由于受其他原因影响,在实际加工过程中,A生产线每小时比原计划少加工100个,B生产线每小时比原计划少加工50个.为了尽快将粽子投放到市场,A生产线每天比原计划多加工3小时,B生产线每天比原计划多加工![]() a小时.这样每天加工的粽子不少于6300个,求a的最小值.
a小时.这样每天加工的粽子不少于6300个,求a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米80元,试问铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,△ACE是等腰三角形,∠AEC=120°,AE=CE,F为BC中点,连接AE.
(1)直接写出∠BAE的度数为 ;
(2)判断AF与CE的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系中,A(0,﹣1)、B(﹣2,0)C(4,0)
(1)求△ABC的面积;
(2)在y轴上是否存在一个点D,使得△ABD为等腰三角形,若存在,求出点D坐标;若不存,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明:小强想证明下面的问题:“有两个角(图中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的
)相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的![]() 和边
和边![]() .
.
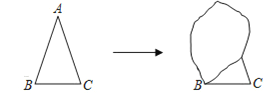
(1)请问:他能够把图恢复成原来的样子吗?若能,请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子.

(2)你能够证明这样的三角形是等腰三角形吗?(至少用两种方法证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).对于下列命题:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正确的有____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
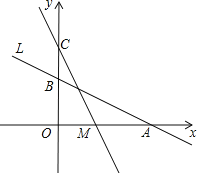
【题目】如图,直线L:y=﹣![]() x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,请直接写出此时t值和M点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com