
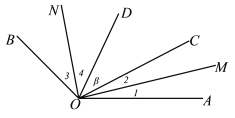
【题目】如图,射线OC、OD在∠AOB内部,∠AOB=![]() ,∠COD=
,∠COD=![]() ,分别作∠AOC和∠BOD的平分线OM、ON,
,分别作∠AOC和∠BOD的平分线OM、ON,
(1)当![]() =130°,
=130°,![]() =40°时,请你填空:∠1+∠3=______°,∠MON=______°;
=40°时,请你填空:∠1+∠3=______°,∠MON=______°;
(2)聪明的小芳通过探究发现,当射线OC、OD的位置在∠AOB内变化时,∠MON与![]() 、
、![]() 之间总满足∠MON=
之间总满足∠MON=![]() ,你是否认同她的这一结论?请说明理由;
,你是否认同她的这一结论?请说明理由;
【答案】(1)45°;85°;(2)是,理由见解析
【解析】
(1)先求出∠BOD+∠AOC,然后根据角平分线的定义可得∠3=∠4=![]() ∠BOD,∠1=∠2=
∠BOD,∠1=∠2=![]() ∠AOC,从而求出∠1+∠3和∠2+∠4,即可求出∠MON;
∠AOC,从而求出∠1+∠3和∠2+∠4,即可求出∠MON;
(2)先求出∠BOD+∠AOC,然后根据角平分线的定义可得∠4=![]() ∠BOD,∠2=
∠BOD,∠2=![]() ∠AOC,从而求出∠2+∠4,即可求出∠MON;
∠AOC,从而求出∠2+∠4,即可求出∠MON;
解:(1)∵∠AOB=![]() =130°,∠COD=
=130°,∠COD=![]() =40°
=40°
∴∠BOD+∠AOC=∠AOB-∠COD=90°
∵ON、OM分别平分∠BOD和∠AOC
∴∠3=∠4=![]() ∠BOD,∠1=∠2=
∠BOD,∠1=∠2=![]() ∠AOC
∠AOC
∴∠1+∠3=∠2+∠4=![]() ∠AOC +
∠AOC +![]() ∠BOD
∠BOD
=![]() (∠AOC +∠BOD)
(∠AOC +∠BOD)
=![]() ×90°
×90°
=45°
∴∠MON=∠2+∠4+∠COD
=45°+40°
=85°
故答案为:45°;85°;
(2)是,理由如下:
∵∠AOB=![]() ,∠COD=
,∠COD=![]()
∴∠BOD+∠AOC=∠AOB-∠COD=![]() -
-![]()
∵ON、OM分别平分∠BOD和∠AOC
∴∠4=![]() ∠BOD,∠2=
∠BOD,∠2=![]() ∠AOC
∠AOC
∴∠2+∠4=![]() ∠AOC +
∠AOC +![]() ∠BOD
∠BOD
=![]() (∠AOC +∠BOD)
(∠AOC +∠BOD)
=![]()
∴∠MON=∠2+∠4+∠COD
=![]() +
+![]()
=![]()


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
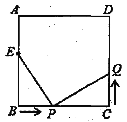
(1)若点Q的运动速度与点P的运动速度相等,经过 秒后,△BPE≌△CQP;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】镇政府想了解李家庄 130 户家庭的经济情况,从中随机抽取了部分家庭进行调查,获得了他们的年收入(单位:万元),并对数据(年收入)进行整理、描述和分析.下面给出了部分信息.
a.被抽取的部分家庭年收入的频数分布直方图和扇形统计图如下(数据分组:0.9≤x<1.3,1.3≤x<1.7 , 1.7≤x<2.1, 2.1≤x<2.5, 2.5≤x<2.9 , 2.9≤x<3.3 )
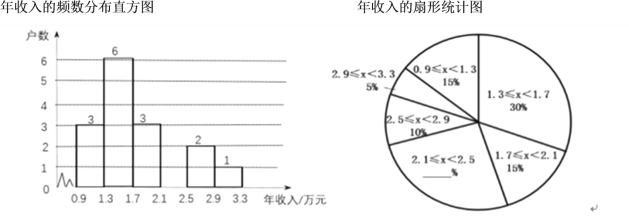
b.家庭年收入在1.3≤x<1.7 这一组的是: 1.3 1.3 1.4 1.5 1.6 1.6
根据以上信息,完成下列问题:
(1)将两个统计图补充完整;
(2)估计李家庄有多少户家庭年收入不低于 1.5 万元且不足 2.1 万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
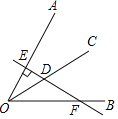
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“三农”问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )
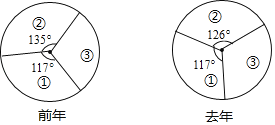
A. ①的收入去年和前年相同
B. ③的收入所占比例前年的比去年的大
C. 去年②的收入为2.8万
D. 前年年收入不止①②③三种农作物的收入
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
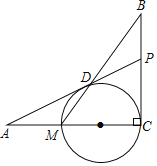
【题目】如图,已知BC⊥AC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且![]() .
.
(1)求证:PD是⊙O的切线;
(2)若AD=12,AM=MC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是__.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com