
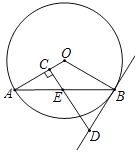
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.
【答案】(1)证明见解析;(2)27.
【解析】(1)根据等腰三角形的性质和切线的判定方法可以求得∠OBD的度数,从而可以证明结论成立;
(2)要求△AOB的面积只要求出OE的长即可,根据题目中的条件和三角形相似的知识可以求得OE的长,从而可以解答本题.
(1)∵OA=OB,DB=DE,
∴∠A=∠OBA,∠DEB=∠DBE,
∵EC⊥OA,∠DEB=∠AEC,
∴∠A+∠DEB=90°,
∴∠OBA+∠DBE=90°,
∴∠OBD=90°,
∵OB是圆的半径,
∴BD是⊙O的切线;
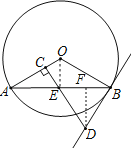
(2)过点D作DF⊥AB于点F,连接OE,
∵点E是AB的中点,AB=12,
∴AE=EB=6,OE⊥AB,
又∵DE=DB,DF⊥BE,DB=5,DB=DE,
∴EF=BF=3,
∴DF=![]() =4,
=4,
∵∠AEC=∠DEF,
∴∠A=∠EDF,
∵OE⊥AB,DF⊥AB,
∴∠AEO=∠DFE=90°,
∴△AEO∽△DFE,
∴![]() ,
,
即![]() ,得EO=4.5,
,得EO=4.5,
∴△AOB的面积是:![]() =27.
=27.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的网格中有四条线段AB、CD、EF、GH(线段端点在格点上),
⑴选取其中三条线段,使得这三条线段能围成一个直角三角形.
答:选取的三条线段为 .
⑵只变动其中两条线段的位置,在原图中画出一个满足上题的直角三角形(顶点仍在格点,并标上必要的字母).
答:画出的直角三角形为△ .
⑶所画直角三角形的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
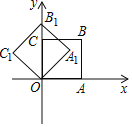
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
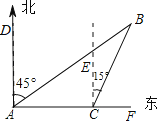
【题目】如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20![]() 海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:
海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD为∠ABC的平分线,DE⊥BC于E,且AB+BC=2BE.
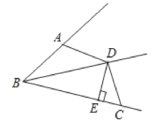
(1)求证:∠BAD+∠BCD=180°;
(2)若将条件“AB+BC=2BE”与结论“∠BAD+∠BCD=180°”互换,结论还成立吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表三行数的规律,回答下列问题:
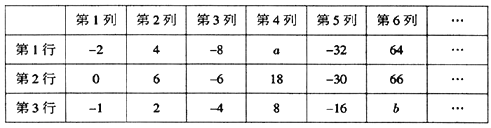
(1)第1行的第四个数a是多少;第3行的第六个数b是多少;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为多少;
(3)巳知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
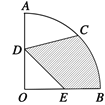
【题目】如图,在圆心角为 ![]() 的扇形
的扇形 ![]() 中,半径
中,半径 ![]() =4cm,
=4cm,![]() 为弧
为弧 ![]() 的中点,
的中点,![]() ,
,![]() 分别是
分别是 ![]() ,
,![]() 的中点,则图中阴影部分的面积(单位
的中点,则图中阴影部分的面积(单位![]() )为( )
)为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
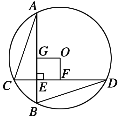
【题目】如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1、A2、A3……在射线ON上,点B1、B2、B3……在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4……均为等边三角形,且OA1=1.
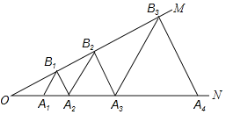
(1)分别求出△A1B1A2、△A3B3A4的边长;
(2)求△A7B7A8的周长(直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com