
【题目】如图,⊙O的半径为5,弦AB⊥CD于E,AB=CD=8.
(1)求证:AC=BD;
(2)若OF⊥CD于F,OG⊥AB于G,试说明四边形OFEG是正方形;
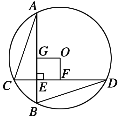
【答案】(1)证明见解析;(2)四边形OFEG是正方形,理由见解析.
【解析】
(1)根据圆心角、弧、弦的关系先由AB=CD判断![]() ,再得到
,再得到![]() ,从而判断AC=BD;
,从而判断AC=BD;
(2)先证明四边形OFEG为矩形,连结OA、OD,如图,再根据垂径定理得到CF=DF,AG=BG,则利用CD=AB得到AG=DF,然后根据正方形的判定方法可判断四边形OFEG是正方形;
(1)证明:∵AB=CD,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴AC=BD
(2)四边形OFEG是正方形
理由如下:
如图,连接OA、OD.
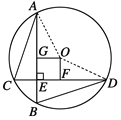
∵AB⊥CD,OF⊥CD,OG⊥AB,
∴四边形OFEG是矩形,DF=![]() CD,AG=
CD,AG=![]() AB.
AB.
∵AB=CD,
∴DF=AG.
∵OD=OA,
∴OD=OA,
∴△OFD≌△OGA,
∴OF=OG.
∴矩形OFEG是正方形


科目:初中数学 来源: 题型:
【题目】已知变量x、y对应关系如下表已知值呈现的对应规律.
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | 4 | … |
y | … |
|
| 1 | 2 | ﹣2 | ﹣1 | ﹣ | ﹣ | … |
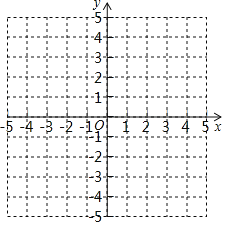
(1)依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
(2)在这个函数图象上有一点P(x,y)(x<0),过点P分别作x轴和y轴的垂线,并延长与直线y=x﹣2交于A、B两点,若△PAB的面积等于![]() ,求出P点坐标.
,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
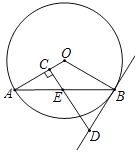
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
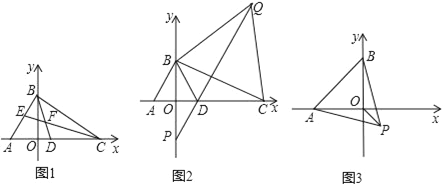
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级的同学参加了一项“节能环保”的社会调查活动,为了了解家庭用电的情况,他们随机调查了某城区50 个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).

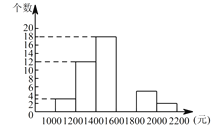
请你根据以上提供的信息,解答下列问题:
(1)频数分布表中 ![]() ________________,
________________,![]() ________________,
________________,
(2)补全频数分布直方图;
(3)这 ![]() 个家庭电费支出的中位数落在________组内;
个家庭电费支出的中位数落在________组内;
(4)若该城区有 ![]() 万个家庭,请你估计该城区有多少个一年电费支出低于
万个家庭,请你估计该城区有多少个一年电费支出低于 ![]() 元的家庭?
元的家庭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】景山中学组织七年级师生春游,如果单独租用45座客车若干辆,则刚好坐满;如果单独租用60座客车,则可少租1辆,并且剩余15个座位.
(1)求参加春游的人数?
(2)已知45座客车的日租金为每辆250元,60座客车的日租金为每辆300元,
问:租用哪种车更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“万州古红桔”原名“万县红桔”,古称丹桔(以下简称为红桔),种植距今至少已有一千多年的历史,“玫瑰香橙”(源自意大利西西里岛塔罗科血橙,以下简称香橙)现已是万州柑橘发展的主推品种之一.某水果店老板在2017年11月份用15200元购进了400千克红桔和600千克香橙,已知香橙的每千克进价比红桔的每千克进价2倍还多4元.
(1)求11月份这两种水果的进价分别为每千克多少元?
(2)时下正值柑橘销售旺季,水果店老板决定在12月份继续购进这两种水果,但进入12月份,由于柑橘的大量上市,红桔和香橙的进价都有大幅下滑,红桔每千克的进价在11月份的基础上下降了![]() m%,香橙每千克的进价在11月份的基础上下降了m%,由于红桔和“玫瑰香橙”都深受库区人民欢迎,实际水果店老板在12月份购进的红桔数量比11月份增加了
m%,香橙每千克的进价在11月份的基础上下降了m%,由于红桔和“玫瑰香橙”都深受库区人民欢迎,实际水果店老板在12月份购进的红桔数量比11月份增加了![]() m%,香橙购进的数量比11月份增加了2m%,结果12月份所购进的这两种柑橘的总价与11月份所购进的这两种柑橘的总价相同,求m的值.
m%,香橙购进的数量比11月份增加了2m%,结果12月份所购进的这两种柑橘的总价与11月份所购进的这两种柑橘的总价相同,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的方程组
的方程组![]() 以下结论:①当
以下结论:①当![]() 时,方程组的解也是方程
时,方程组的解也是方程![]() 的解;②存在实数
的解;②存在实数![]() ,使得
,使得![]() ;③当
;③当![]() 时,
时,![]() ;④不论
;④不论![]() 取什么实数,
取什么实数,![]() 的值始终不变,其中正确的是( )
的值始终不变,其中正确的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为![]() 千克,烤制时间为
千克,烤制时间为![]() ,估计当
,估计当![]() 千克时,
千克时,![]() 的值为( )
的值为( )
A.138B.140C.148D.160
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com