
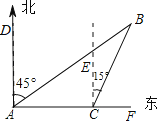
【题目】如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20![]() 海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:
海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】A处与灯塔B相距109海里.
【解析】直接过点C作CM⊥AB求出AM,CM的长,再利用锐角三角函数关系得出BM的长即可得出答案.
过点C作CM⊥AB,垂足为M,
在Rt△ACM中,∠MAC=90°﹣45°=45°,则∠MCA=45°,
∴AM=MC,
由勾股定理得:AM2+MC2=AC2=(20![]() ×2)2,
×2)2,
解得:AM=CM=40,
∵∠ECB=15°,
∴∠BCF=90°﹣15°=75°,
∴∠B=∠BCF﹣∠MAC=75°﹣45°=30°,
在Rt△BCM中,tanB=tan30°=![]() ,即
,即![]() ,
,
∴BM=40![]() ,
,
∴AB=AM+BM=40+40![]() ≈40+40×1.73≈109(海里),
≈40+40×1.73≈109(海里),
答:A处与灯塔B相距109海里.



科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上,从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t秒。
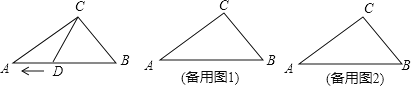
(1)点D在运动t秒后,BD= cm(用含有t的式子表示)
(2)AB=cm,AB边上的高为cm;
(3)点D在运动过程中,当△BCD为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知变量x、y对应关系如下表已知值呈现的对应规律.
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | 4 | … |
y | … |
|
| 1 | 2 | ﹣2 | ﹣1 | ﹣ | ﹣ | … |
(1)依据表中给出的对应关系写出函数解析式,并在给出的坐标系中画出大致图象;
(2)在这个函数图象上有一点P(x,y)(x<0),过点P分别作x轴和y轴的垂线,并延长与直线y=x﹣2交于A、B两点,若△PAB的面积等于![]() ,求出P点坐标.
,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知l1∥l2,点A,B在l1上,点C,D在l2上,连接AD,BC.AE,CE分别是∠BAD,∠BCD的角平分线,∠α=70°,∠β=30°.
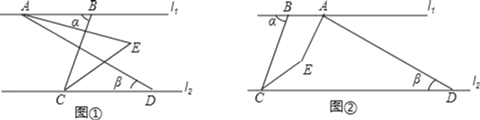
(1)如图①,求∠AEC的度数;
(2)如图②,将线段AD沿CD方向平移,其他条件不变,求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,且∠DOE=60°,∠BOE=![]() ∠EOC,则下列四个结论正确的有__________
∠EOC,则下列四个结论正确的有__________
①∠BOD=30°;②射线OE平分∠AOC;③图中与∠BOE互余的角有2个;④图中互补的角有6对.
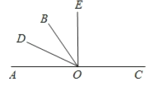
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.
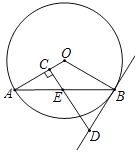
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
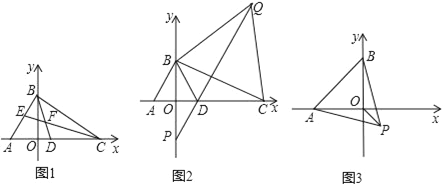
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的方程组
的方程组![]() 以下结论:①当
以下结论:①当![]() 时,方程组的解也是方程
时,方程组的解也是方程![]() 的解;②存在实数
的解;②存在实数![]() ,使得
,使得![]() ;③当
;③当![]() 时,
时,![]() ;④不论
;④不论![]() 取什么实数,
取什么实数,![]() 的值始终不变,其中正确的是( )
的值始终不变,其中正确的是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com