
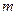 ,
, 上任意两点,C是直线
上任意两点,C是直线 上一点,且
上一点,且 AB (k≠0).
AB (k≠0). =1
=1 时,在图(1)中,作∠BEF=∠ABC,EF交直线
时,在图(1)中,作∠BEF=∠ABC,EF交直线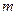 于点F.,写出线段EF与
于点F.,写出线段EF与 ≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由. . ……………………………………………2分
. ……………………………………………2分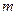 上截取
上截取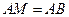 ,连结
,连结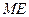 .
.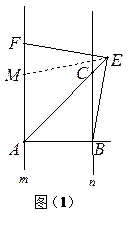
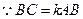 ,
,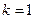 ,
,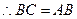 .
. ,
,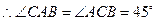 .
.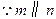 ,
,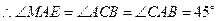 ,
,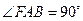 .
.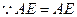 ,
,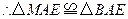 .·························· 3分
.·························· 3分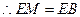 ,
,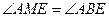 .……………………………4分
.……………………………4分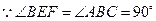 ,
,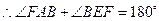 .
.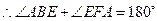 .又
.又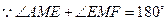 ,
,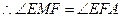 .
.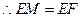 .
.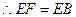 .…………
.………… ………….………………………………..5分
………….………………………………..5分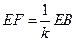 .
.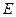 作
作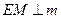 ,
, ,垂足为
,垂足为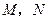 .
.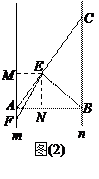
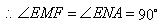 .
.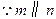 ,
,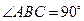 ,
,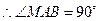 .
.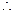 四边形
四边形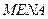 为矩形.
为矩形.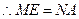 ,
,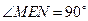 .
.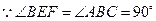 ,
,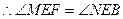 .
.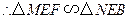 .·············································································· 6分
.·············································································· 6分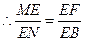 .
.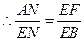 .
.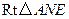 和
和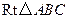 中,
中,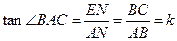 ,
,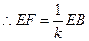 .………………………………………………………………………………7分
.………………………………………………………………………………7分

科目:初中数学 来源:不详 题型:解答题
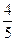 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
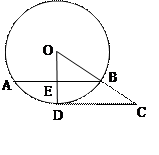
 ,BC=4.点M是AC上动点(与点A不重合),设AM=x,过点M作AC的垂线,交直线AB于点N.
,BC=4.点M是AC上动点(与点A不重合),设AM=x,过点M作AC的垂线,交直线AB于点N.
 ?若能,请求出此时x的值,若不能,请说明理由.
?若能,请求出此时x的值,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,点E是AB的中点,过点E作DE⊥AB交BC于点D,联结AD,若AC=8,
,点E是AB的中点,过点E作DE⊥AB交BC于点D,联结AD,若AC=8, .
.
 的长;
的长;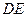 的长.
的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ),直接写出y与t之间的函数关系式;
),直接写出y与t之间的函数关系式;


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 确到0.1米;参考数据
确到0.1米;参考数据 ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com