
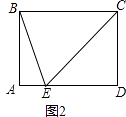
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC
(1)如图1,判断△BCE的形状,并说明理由; 
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长. 
【答案】
(1)解:如图1中,结论:△BCE是等腰三角形.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠CBE=∠AEB,
∵BE平分∠AEC,
∴∠AEB=∠BEC,
∴∠CBE=∠BEC,
∴CB=CE,
∴△CBE是等腰三角形.

(2)解:如图2中,∵四边形ABCD是平行四边形,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠D=90°,BC=AD=5,
在RT△ECD中,∵∠D=90°,ED=AD﹣AE=4,EC=BC=5,
∴AB=CD= ![]() =
= ![]() =3,
=3,
在RT△AEB中,∵∠A=90°AB=3.AE=1,
∴BE= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)结论:△BCE是等腰三角形,根据平行四边形的性质以及已知条件,只要证明∠CBE=∠BEC即可.(2)先证明四边形ABCD是矩形,然后分别在RT△ECD,和RT△ABE中利用勾股定理即可解决问题.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A. 
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
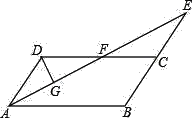
【题目】如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若AB=4,点F为DC的中点,DG⊥AE,垂足为G,且DG=1,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=AC.

(1)求∠CDE的度数;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=2x+1与双曲线y= ![]() 的一个交点为A(m,﹣3).
的一个交点为A(m,﹣3).
(1)求双曲线的表达式;
(2)过动点P(n,0)(n<0)且垂直于x轴的直线与直线y=2x+1和双曲线y= ![]() 的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
的交点分别为B,C,当点B位于点C上方时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
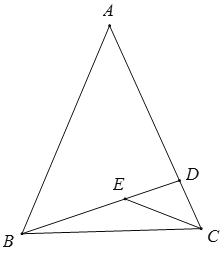
【题目】如图,在△ABC中,BD⊥AC于D.若∠A:∠ABC:∠ACB=3:4:5,E为线段BD上任一点.
(1)试求∠ABD的度数;
(2)求证:∠BEC>∠A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx﹣2(k>0)与双曲线 ![]() 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 . 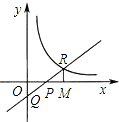
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com