
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.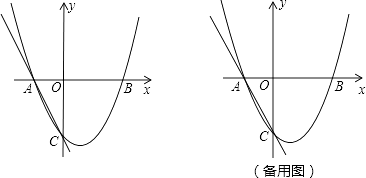
(1)求二次函数的解析式;
(2)点P在x轴正半轴上,且PA=PC,求OP的长;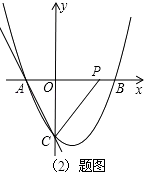
(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.
①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;
②若⊙M的半径为 ![]() ,求点M的坐标.
,求点M的坐标.
【答案】
(1)
解:设该二次函数的解析式为:y=a(x+1)(x﹣2),
将x=0,y=﹣2代入,得﹣2=a(0+1)(0﹣2),
解得a=1,
∴抛物线的解析式为y=(x+1)(x﹣2),
即y=x2﹣x﹣2
(2)
解:设OP=x,则PC=PA=x+1,
在Rt△POC中,由勾股定理,得x2+22=(x+1)2,
解得,x= ![]() ,
,
即OP= ![]()
(3)
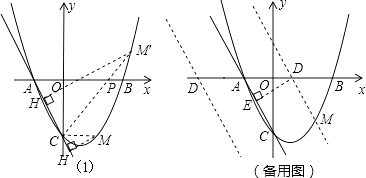
解:①∵△CHM∽△AOC,
∴∠MCH=∠CAO,
(i)如图1,当H在点C下方时,
∵∠OAC+∠OCA=90°,∠MCH=∠OAC
∴∠OCA+∠MCH=90°
∴∠OCM=90°=∠AOC
∴CM∥x轴
∴yM=﹣2,
∴x2﹣x﹣2=﹣2,
解得x1=0(舍去),x2=1,
∴M(1,﹣2),
(ii)如图1,当H在点C上方时,
∵∠MCH=∠CAO,
∴PA=PC,由(2)得,M′为直线CP与抛物线的另一交点,
设直线CM′的解析式为y=kx﹣2,
把P( ![]() ,0)的坐标代入,得
,0)的坐标代入,得 ![]() k﹣2=0,
k﹣2=0,
解得k= ![]() ,
,
∴y= ![]() x﹣2,
x﹣2,
由 ![]() x﹣2=x2﹣x﹣2,
x﹣2=x2﹣x﹣2,
解得x1=0(舍去),x2= ![]() ,
,
此时y= ![]() ×
× ![]() ﹣2=
﹣2= ![]() ,
,
∴M′( ![]() ,
, ![]() ),
),
②在x轴上取一点D,如图(备用图),过点D作DE⊥AC于点E,使DE= ![]() ,
,
在Rt△AOC中,AC= ![]() =
= ![]() =
= ![]() ,
,
∵∠COA=∠DEA=90°,∠OAC=∠EAD,
∴△AED∽△AOC,
∴ ![]() ,
,
即 ![]() =
= ![]() ,
,
解得AD=2,
∴D(1,0)或D(﹣3,0).
过点D作DM∥AC,交抛物线于M,如图(备用图)
则直线DM的解析式为:y=﹣2x+2或y=﹣2x﹣6,
当﹣2x﹣6=x2﹣x﹣2时,即x2+x+4=0,方程无实数根,
当﹣2x+2=x2﹣x﹣2时,即x2+x﹣4=0,解得x1= ![]() ,x2=
,x2= ![]() ,
,
∴点M的坐标为( ![]() ,3+
,3+ ![]() )或(
)或( ![]() ,3﹣
,3﹣ ![]() )
)  .
.
【解析】(1)根据与x轴的两个交点A、B的坐标,设出二次函数交点式解析式y=a(x+1)(x﹣2),然后把点C的坐标代入计算求出a的值,即可得到二次函数解析式;(2)设OP=x,然后表示出PC、PA的长度,在Rt△POC中,利用勾股定理列式,然后解方程即可;(3)①根据相似三角形对应角相等可得∠MCH=∠CAO,然后分(i)点H在点C下方时,利用同位角相等,两直线平行判定CM∥x轴,从而得到点M的纵坐标与点C的纵坐标相同,是﹣2,代入抛物线解析式计算即可;(ii)点H在点C上方时,根据(2)的结论,点M为直线PC与抛物线的另一交点,求出直线PC的解析式,与抛物线的解析式联立求解即可得到点M的坐标;②在x轴上取一点D,过点D作DE⊥AC于点E,可以证明△AED和△AOC相似,根据相似三角形对应边成比例列式求解即可得到AD的长度,然后分点D在点A的左边与右边两种情况求出OD的长度,从而得到点D的坐标,再作直线DM∥AC,然后求出直线DM的解析式,与抛物线解析式联立求解即可得到点M的坐标.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】(1)已知2x﹣1的平方根是±6,2x+y﹣1的算术平方根是5,求2x﹣3y+11的立方根.
(2)已知x是1的平方根,求代数式(x2017﹣1)(x2018﹣712)(x2019+1)(x2020+712)+1000x的立方根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
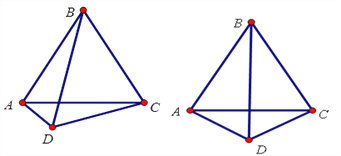
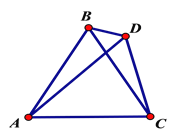
【题目】如图,△ABC是等边三角形,D是三角形外一动点,满足∠ADB=600,
(1)当D点在AC的垂直平分线上时,求证: DA+DC=DB.
(2)当D点不在AC的垂直平分线上时,(1)中的结论是否仍然成立?请说明理由.
(3)当D点在如图的位置时,直接写出DA,DC,DB的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
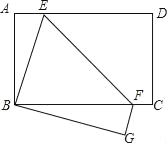
【题目】已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF、射线ED分别交于点M、N,当EN=MN时,则FM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】检修队乘汽车沿着东西走向的公路往返行驶检修线路.某天早上从A地出发到收工时所走的路线为(若约定向东为正方向),当天行驶的记录如下:(单位:km)
+18,﹣9.5,+7,﹣14,﹣6.2,+13,﹣6.8,+10.5.
(1)收工时距A地多远?
(2)若汽车行驶每千米耗油0.3升,那么这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
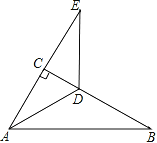
【题目】如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
(1)求证:DE=DB;
(2)连接BE,试判断△ABE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰RtABC 中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连接PC,若△ABC的面积为8cm2,则△BPC的面积为( )

A. 4cm2 B. 5cm2 C. 6cm2 D. 7cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com