
【题目】如图,已知∠AGE+∠AHF=180°,∠BEC=∠BFC,则∠A与∠D相等吗?下面是童威同学的推导过程,请你帮助他在括号内填上推导依据 ∵∠AGE+∠AHF=180°(已知)
∠AGE=∠CGD ()
∴∠CGD+∠AHF=180°
∴CE∥BF ()
∴∠BEC+∠B=180°
∵∠BFC+∠BFD=180°
∠BEC=∠BFC(已知)
∴∠B=∠BFD ()
∴AB∥CD
∴∠A=∠D.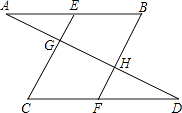
【答案】对顶角相等;同旁内角互补,两直线平行;同角的补角相等
【解析】解:∵∠AGE+∠AHF=180°(已知), ∠AGE=∠CGD (对顶角相等),
∴∠CGD+∠AHF=180°,
∴CE∥BF (同旁内角互补,两直线平行),
∴∠BEC+∠B=180°,
∵∠BFC+∠BFD=180°,
∠BEC=∠BFC(已知),
∴∠B=∠BFD (同角的补角相等),
∴AB∥CD,
∴∠A=∠D,
所以答案是:对顶角相等,同旁内角互补,两直线平行,同角的补角相等.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:

且![]() =8,
=8,![]() =1.8,根据上述信息完成下列问题:
=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是 ,中位数是 .
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
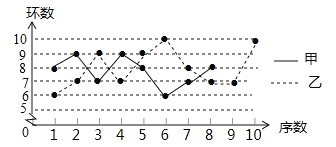
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中去括号正确的是( )
A. a+(b-c+d)=a-b+c-d B. a-(b-c+d)=a-b-c+d
C. a-(b-c+d)=a-b+c-d D. a-(b-c+d)=a-b+c+d
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是 . 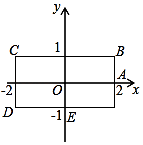
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com