
【题目】如图,已知抛物线y=x2+bx+c与x轴相交于点A(1,0)和点B,与y轴交于点C(0,﹣3)顶点为D
(1)求抛物线的函数关系式;
(2)判断△BCD的形状,并说明理由;
(3)点P在抛物线上,点Q在直线y=x上,是否存在点P、Q使以点P、Q、C、O为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
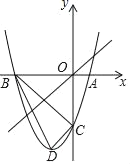
【答案】(1)y=x2+2x﹣3,顶点D的坐标为(﹣1,﹣4);(2)△BCD为直角三角形,理由详见解析;(3)存在,点P(﹣1,4)或(2,5).
【解析】
(1)把点A、C坐标代入抛物线表达式,即可求解;
(2)BD=![]() ,CD=
,CD=![]() ,BC=
,BC=![]() ,由勾股定理的逆定理即可求解;
,由勾股定理的逆定理即可求解;
(3)分OC是平行四边形的一条边、CO是平行四边形的对角线两种情况,分别求解即可.
(1)把点A、C坐标代入抛物线表达式得:![]() ,解得:
,解得:![]() ,
,
抛物线的表达式为:y=x2+2x﹣3,
顶点D的坐标为(﹣1,﹣4);
(2)y=x2+2x﹣3,令y=0,则x=1或﹣3,故点B(﹣3,0),而C、D的坐标分别为:(0,﹣3)、(﹣1,﹣4),
则BD=![]() ,CD=
,CD=![]() ,BC=
,BC=![]() ,
,
故:BD2=CD2+BC2,
故△BCD为直角三角形;
(3)存在,理由:
①当OC是平行四边形的一条边时,
设:点P(m,m2+2m﹣3),点Q(m,m),
则PQ=OC=3,
PQ=|m2+2m﹣3﹣m|=3,
解得:m=﹣1或2或0或﹣3(舍去0、﹣3),
故m=﹣1或2;
②当CO是平行四边形的对角线时,
设点P(m,m2+2m﹣3),点Q(n,n),
由中线定理得:![]() ,
,
解得:m=0或﹣1(舍去0);
故m=﹣1或2,
则点P(﹣1,-4)或(2,5).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象相交于A(2n+1,1),B(﹣1,n﹣4)两点,与y轴相交于点C
的图象相交于A(2n+1,1),B(﹣1,n﹣4)两点,与y轴相交于点C
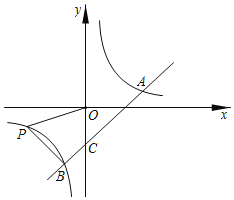
(1)反比例函数的解析式为_____,一次函数的解析式为_____;
(2)请直接写出不等式kx+b≥![]() 的解集;
的解集;
(3)过点B作BP⊥AB,交反比例函数![]() (x<0)的图象于点P,连接OP,求四边形OPBC的面积.
(x<0)的图象于点P,连接OP,求四边形OPBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
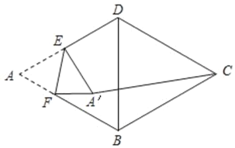
【题目】如图,BD是菱形ABCD的对角线,E是边AD的中点,F是边AB上的一点,将△AEF沿EF所在的直线翻折得到△A′EF,连结A′C.若AB=5,BD=6,当点A′到∠A的两边的距离相等时,A′C的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+4x+c(a≠0)的图象与x轴交A,B两点,与y轴交于点C,直线y=﹣2x﹣6经过点A,C.
(1)求该二次函数的解析式;
(2)点P为第三象限内抛物线上的一个动点,△APC的面积为S,试求S的最大值;
(3)若P为抛物线的顶点,且直角三角形APQ的直角顶点Q在y轴上,请直接写出点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
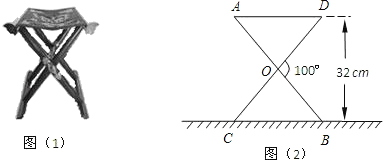
【题目】某大学计划为新生配备如图(1)所示的折叠椅.图(2)是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32cm,∠DOB=100°,那么椅腿的长AB和篷布面的宽AD各应设计为多少cm?(结果精确到0.1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
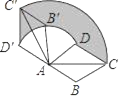
【题目】如图,在菱形ABCD中,AB=2,∠BAC=30°,将菱形ABCD绕点A逆时针旋转120°,点B的对应点为点B′,点C的对应点为点C′,点D的对应点为点D′,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() 与y轴交于A,与x轴交于D,抛物线y=
与y轴交于A,与x轴交于D,抛物线y=![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
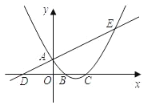
(1)求抛物线的解析式;
(2)点P是直线AE上一动点,当△PBC周长最小时,求点P坐标;
(3)动点Q在x轴上移动,当△QAE是直角三角形时,求点Q的坐标;
(4)在y轴上是否存在一点M,使得点M到C点的距离与到直线AD的距离恰好相等?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
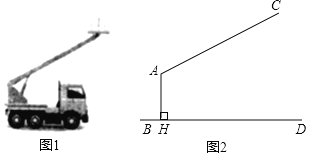
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com