
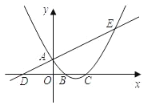
【题目】已知:直线![]() 与y轴交于A,与x轴交于D,抛物线y=
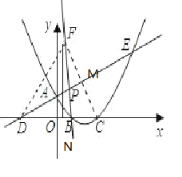
与y轴交于A,与x轴交于D,抛物线y=![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
(1)求抛物线的解析式;
(2)点P是直线AE上一动点,当△PBC周长最小时,求点P坐标;
(3)动点Q在x轴上移动,当△QAE是直角三角形时,求点Q的坐标;
(4)在y轴上是否存在一点M,使得点M到C点的距离与到直线AD的距离恰好相等?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,
,![]() );(3)Q点坐标为(1,0)或(
);(3)Q点坐标为(1,0)或(![]() ,0);(4)存在;M点坐标为M(0,﹣8).
,0);(4)存在;M点坐标为M(0,﹣8).
【解析】
(1)求解抛物线的解析式关键是找点,然后将点的坐标带入解析式即可求出解析式;已知B点的坐标,已知A点是直线与抛物线的交点且交于y轴,即可通过直线的解析式求出A点坐标,带入A,B两点坐标即可;(2)最值问题的关键是找对称,通过C点作关于直线AE的对称点F,再连接BF,交AE与点P,此时△PBC周长最小;再求出BF的解析式,再求出与直线AE的交点即可;(3)设出P点的坐标,然后表示出AP、EP的长,求出AE 的长,利用勾股定理得到有关P点的横坐标的方程,求得其横坐标即可;(4)设出M点的坐标,利用C点的距离与到直线AD的距离恰好相等,得到有关M点的纵坐标的方程解得M点的纵坐标即可。
解:(1)∵直线![]() 与y轴交于A,
与y轴交于A,
∴A点的坐标为(0,2),
∵B点坐标为(1,0).
∴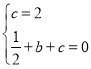 解得:
解得: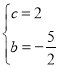
∴![]() ;
;
(2)作出C关于直线AE的对称点F,连接BF,CF分别交AE与点P,M,连接DF.过点F做FN垂直于X轴,交X轴于点N.
由题意得点C的坐标为![]() ,点D的坐标为
,点D的坐标为![]()
∵点F是点C关于直线AE的对称点,
∴AE垂直平分CF,
∴直线AE与直线CF的解析式的k值之积为-1,可设直线CF的解析式为![]()
将C点坐标带入可求得CF的解析式为:![]()
将CF和AE的解析式联立可得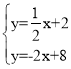 ,解得
,解得![]()
从而求出直线AE与CF的交点M坐标为![]() ,
,
∵M点为CF中点,
所以F点的纵坐标为![]() ,即
,即![]()
∵△CDF为等腰三角形,∴![]()
∴在直角三角形DFN中,由勾股定理得:![]()
∴得![]()
∴N点横坐标为![]()
∴F点的坐标为![]()
∴直线BF的解析式为:![]() ,
,
 ,
,
可得:P(![]() ,
,![]() );
);
(3)根据题意得:![]() ,
,
解得:![]() 或
或![]() ,
,
∴A(0,2),E(6,5),
∴![]() ,
,
设Q(x,0),
①若Q为直角顶点,
则![]() ,
,
即![]() ,
,
此时x无解;
②若点A为直角顶点,
则![]() ,
,
即![]() ,
,
解得:![]() ,
,
即Q(1,0);
③若E为直角顶点,
则![]() ,
,
即![]() ,
,
解得:![]() ,
,
此时求得Q(![]()
![]() ,0);
,0);
∴Q(1,0)或(![]() ,0)
,0)
(4)假设存在,设M坐标为(0,m),则![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴当![]() 时,满足条件,
时,满足条件,
∴在直角三角形AOD中,根据勾股定理得:![]() ,且
,且![]() ,
,![]() ,
,
∵![]() ,
,
∴根据勾股定理得:![]() ,
,
即![]() ,
,
解得![]() ,
,
则M(0,﹣8).


科目:初中数学 来源: 题型:
【题目】红灯笼,象征着阖家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
(1)求甲、乙两种灯笼每对的进价;
(2)经市场调查发现,乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对:物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.
①求出y与x之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
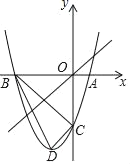
【题目】如图,已知抛物线y=x2+bx+c与x轴相交于点A(1,0)和点B,与y轴交于点C(0,﹣3)顶点为D
(1)求抛物线的函数关系式;
(2)判断△BCD的形状,并说明理由;
(3)点P在抛物线上,点Q在直线y=x上,是否存在点P、Q使以点P、Q、C、O为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
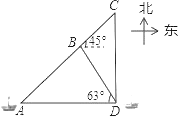
【题目】某渔船向正东方向航行,上午8点在A处时发现渔船、小岛B和小岛C在同一条直线上,渔船以30海里/小时的速度继续向正东方向航行,上午10点到达位于小岛C的正南方向上的D处,此时小岛B在渔船的西偏北63°的方向上,如图,已知小岛C在小岛B的东偏北45°的方向上,求小岛B和小岛C之间的距离.(结果精确到1海里,参考数据:sin63°≈0.9,cos63°≈0.5,tan63°≈2.0,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)(2015春鞍山期末)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | 50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
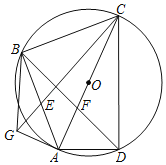
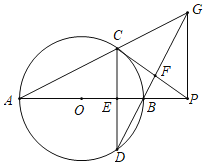
【题目】如图,四边形ABCD内接于以AC为直径的⊙O,AD=![]() ,CD=2
,CD=2![]() ,BC=BA,AC与BD相交于点F,将△ABF沿AB翻折,得到△ABG,连接CG交AB于E,则BE长为_____.
,BC=BA,AC与BD相交于点F,将△ABF沿AB翻折,得到△ABG,连接CG交AB于E,则BE长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P是AB延长线上一点,连接PC交DB的延长线于点F,且∠PFB=3∠CAB.
(1)求证:PC是⊙O的切线;
(2)延长AC,DF相交于点G,连接PG,请探究∠CPG和∠CAB的数量关系,并说明理由;
(3)若tan∠CAB=![]() ,CF=5,求⊙O的半径.
,CF=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,CD⊥AB于点D.
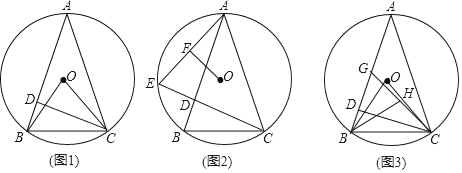
(1)如图1,连接OB和OC,AB=AC,求证:∠BOC=4∠BCD;
(2)如图2,延长CD交⊙O于点E,连接AE,过点O作OF⊥AE,垂足为F,求证:BC=2OF;
(3)如图3,在(1)的条件下,G是AB上一点,连接CG,H为CG的中点,连接BH,若∠BAC=∠HBA,AG=8,BH=9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对该市市民的购物方式进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请根据两幅统计图中提供的信息,解答下列问题:
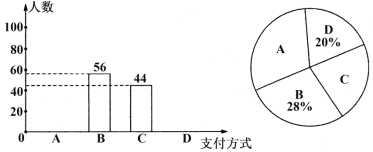
⑴求本次一共调查的购买者人数;
⑵请补全条形统计图;
⑶求在扇形统计图中A种支付方式所对应的圆心角度数;
⑷若该超市一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者大约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com