
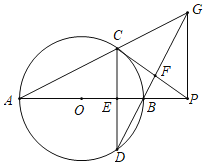
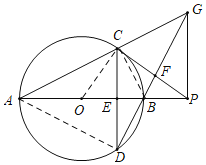
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P是AB延长线上一点,连接PC交DB的延长线于点F,且∠PFB=3∠CAB.
(1)求证:PC是⊙O的切线;
(2)延长AC,DF相交于点G,连接PG,请探究∠CPG和∠CAB的数量关系,并说明理由;
(3)若tan∠CAB=![]() ,CF=5,求⊙O的半径.
,CF=5,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)r=![]()
【解析】
(1)连接OC,由∠PEB=3∠A=∠D+∠DCF,∠D=∠A,得∠DCF=2∠A,∠COB=2∠A,∠DCF=∠COB,因为∠COB+∠OCE=90°,∠DCF+∠OCE=90°,即∠OCP=90°,所以PC是⊙O的切线;
(2)先证明△ACP∽△DCG,所以![]() ,又∠ACD=∠PCG,所以△PCG~△ACD,因此∠CPG=∠CAD=2∠CAB;
,又∠ACD=∠PCG,所以△PCG~△ACD,因此∠CPG=∠CAD=2∠CAB;
(3)由(2)得,PC=PG,∠GPC=∠CAD=∠DCP,所以CD∥PG,于是△GFP~△DFC,又tan∠CAB=![]() ,CF=5,
,CF=5,
设BP=a,PC﹣PG=3a,所以![]() ,CE=
,CE=![]() ,AE=3CE=
,AE=3CE=![]() ,BE=AP﹣BP﹣AE=8a﹣
,BE=AP﹣BP﹣AE=8a﹣![]() ,所以
,所以![]() ,解得
,解得![]() ,所以r=
,所以r=![]() .
.
解:(1)连接OC,
∵∠PEB=3∠A=∠D+∠DCF,
∵∠D=∠A,
∴∠DCF=2∠A,
∴∠COB=2∠A,
∠DCF=∠COB,
∵∠COB+∠OCE=90°,
∴∠DCF+∠OCE=90°,
即∠OCP=90°,
∴PC是⊙O的切线;
(2)∠CPG=2∠CAB.
∵∠BCD=∠CDB=∠CAB=∠ACO,
∠ACP=∠ACO+∠OCP=∠ACO+90°,
∠DCG=∠DCB+∠BCG=∠DCB+90°,
∴∠ACP=∠DCG,
∴△ACP∽△DCG,
∴![]() ,
,
又∵∠ACD=∠PCG,
∴△PCG~△ACD,
∴∠CPG=∠CAD=2∠CAB;
(3)由(2)得,
PC=PG,
∠GPC=∠CAD=∠DCP,
∴CD∥PG,
∴△GFP~△DFC,
∵tan∠CAB=![]() ,CF=5,
,CF=5,
设BP=a,PC﹣PG=3a,
![]() ,
,
![]() ,
,
CE=![]() ,
,
AE=3CE=![]() ,
,
∴BE=AP﹣BP﹣AE=8a﹣![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
AB=8a=![]() ,
,
∴r=![]() .
.


科目:初中数学 来源: 题型:
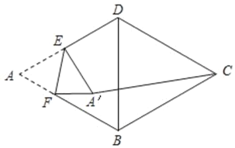
【题目】如图,BD是菱形ABCD的对角线,E是边AD的中点,F是边AB上的一点,将△AEF沿EF所在的直线翻折得到△A′EF,连结A′C.若AB=5,BD=6,当点A′到∠A的两边的距离相等时,A′C的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
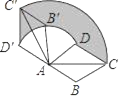
【题目】如图,在菱形ABCD中,AB=2,∠BAC=30°,将菱形ABCD绕点A逆时针旋转120°,点B的对应点为点B′,点C的对应点为点C′,点D的对应点为点D′,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
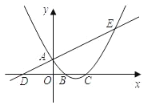
【题目】已知:直线![]() 与y轴交于A,与x轴交于D,抛物线y=
与y轴交于A,与x轴交于D,抛物线y=![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
(1)求抛物线的解析式;
(2)点P是直线AE上一动点,当△PBC周长最小时,求点P坐标;
(3)动点Q在x轴上移动,当△QAE是直角三角形时,求点Q的坐标;
(4)在y轴上是否存在一点M,使得点M到C点的距离与到直线AD的距离恰好相等?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E,F分别是边AB,AD上的点,连接CE,CF并延长,分别交DA,BA的廷长线于点H,G.
(1)如图1,若四边形ABCD是菱形,∠ECF=![]() ∠BCD,求证:AC2=AHAG;
∠BCD,求证:AC2=AHAG;
(2)如图2,若四边形ABCD是正方形,∠ECF=45°,BC=4,设AE=x,AG=y,求y与x的函数关系式;
(3)如图3,若四边形ABCD是矩形,AB:AD=1:2,CG=CH,∠GCH=45°,请求tan∠AHG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;

(2)若⊙O半径为1,求菱形ACBP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=3cm.点P从点A出发,以每秒1cm的速度向终点B运动,同时点Q从点B出发,以每秒3cm的速度沿BC﹣CD﹣DA向终点A运动,到达各自终点时停止运动.设动点的运动时间为x秒,△PBQ的面积为ycm2,则能正确表示△PBQ的面积y与时间x的关系的图象是( )
A.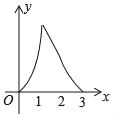 B.
B.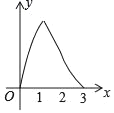
C.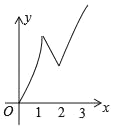 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
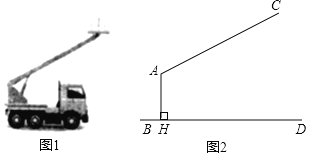
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD纸片中,若沿折痕EG对折,则顶点B落在AD边上的点F处,顶点C落在点N处,点M是FN与DC交点,且AD=8.
(1)当点F是AD的中点时,求△FDM的周长;
(2)当点F不与点A,D和AD的中点重合时,若AE+GD=19,求AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com