
【题目】在正方形ABCD中,AB=3cm.点P从点A出发,以每秒1cm的速度向终点B运动,同时点Q从点B出发,以每秒3cm的速度沿BC﹣CD﹣DA向终点A运动,到达各自终点时停止运动.设动点的运动时间为x秒,△PBQ的面积为ycm2,则能正确表示△PBQ的面积y与时间x的关系的图象是( )
A.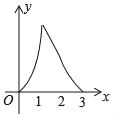 B.
B.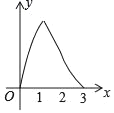
C.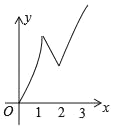 D.
D.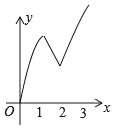
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=![]() 上,点B在双曲线y=
上,点B在双曲线y=![]() (k≠0)上,AB∥x轴,交y轴于点C,若AB=2AC,则k的值为( )
(k≠0)上,AB∥x轴,交y轴于点C,若AB=2AC,则k的值为( )
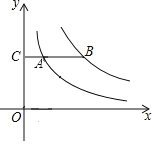
A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)(2015春鞍山期末)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | 50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P是AB延长线上一点,连接PC交DB的延长线于点F,且∠PFB=3∠CAB.
(1)求证:PC是⊙O的切线;
(2)延长AC,DF相交于点G,连接PG,请探究∠CPG和∠CAB的数量关系,并说明理由;
(3)若tan∠CAB=![]() ,CF=5,求⊙O的半径.
,CF=5,求⊙O的半径.
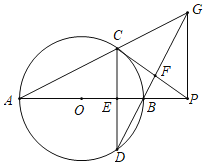
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(提出问题)如图1,在等边三角形ABC内一点P,PA=3,PB=4,PC=5.求∠APB的度数?小明提供了如下思路:
如图2,将△APC绕A点顺时针旋转60°至△AP'B ,则AP'=AP=3,P'C=PB=4,∠P'AC=∠PAB ,所以∠P'AC+∠CAP=∠PAC+∠BAP ,即∠P'AP=∠BAC=60° ,所以△AP'P为等边三角形 ,所以∠A P'P=60° ,
……按照小明的解题思路,
易求得∠APB= ;
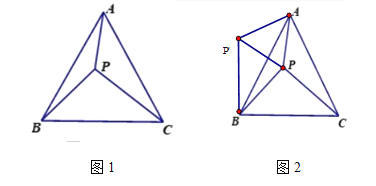
(尝试应用)
如图3,在等边三角形ABC外一点P,PA=6,PB=10,PC=8.求∠APC的度数?
(解决问题)
如图4,平面直角坐标系xoy中,直线AB的解析式为y=-x+b(b>0),在第一象限内一点P,满足PB:PO:PA=1:2:3,则∠BPO= 度(直接写出答案)
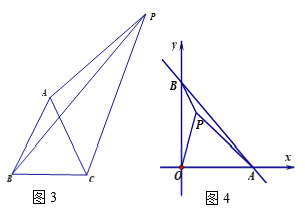
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,CD⊥AB于点D.
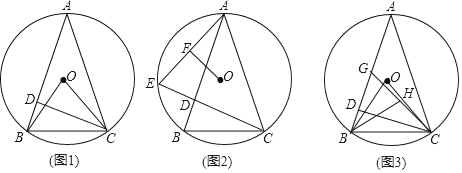
(1)如图1,连接OB和OC,AB=AC,求证:∠BOC=4∠BCD;
(2)如图2,延长CD交⊙O于点E,连接AE,过点O作OF⊥AE,垂足为F,求证:BC=2OF;
(3)如图3,在(1)的条件下,G是AB上一点,连接CG,H为CG的中点,连接BH,若∠BAC=∠HBA,AG=8,BH=9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
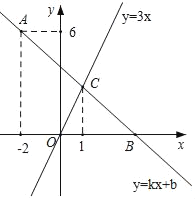
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集.
(3)若点D在y轴上,且满足S△BCD=2S△BOC,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
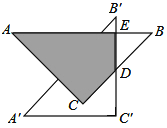
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com