
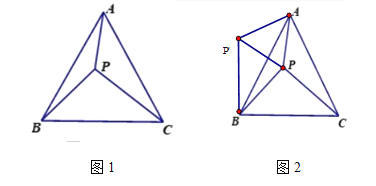
【题目】(提出问题)如图1,在等边三角形ABC内一点P,PA=3,PB=4,PC=5.求∠APB的度数?小明提供了如下思路:
如图2,将△APC绕A点顺时针旋转60°至△AP'B ,则AP'=AP=3,P'C=PB=4,∠P'AC=∠PAB ,所以∠P'AC+∠CAP=∠PAC+∠BAP ,即∠P'AP=∠BAC=60° ,所以△AP'P为等边三角形 ,所以∠A P'P=60° ,
……按照小明的解题思路,
易求得∠APB= ;
(尝试应用)
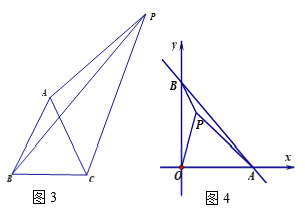
如图3,在等边三角形ABC外一点P,PA=6,PB=10,PC=8.求∠APC的度数?
(解决问题)
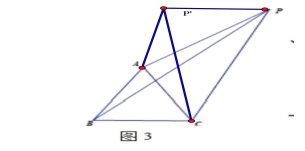
如图4,平面直角坐标系xoy中,直线AB的解析式为y=-x+b(b>0),在第一象限内一点P,满足PB:PO:PA=1:2:3,则∠BPO= 度(直接写出答案)
【答案】【解决问题】 150°;【尝试应用】30°;【解决问题】135°
【解析】
解决问题:由题意得AP'=AP=PP',根据勾股定理的逆定理,可知△P'PB是直角三角形即可求解.
尝试应用:将△ABP绕点A逆时针旋转60°,连接PP',得到△APP'是等边三角形,△PP'C是直角三角形.
解决问题:将△APO绕O逆时针旋转90°,连接PP'证明△PP'O为等腰直角三角形,根据勾股定理证明△PP'B为直角三角形即可.
解决问题:150°.
∵AP'=AP=PP'=3
∴PP'2+BP2= BP'2
∴△BP'P为直角三角形
∴∠APB=150°
尝试应用:∠APC=30°,提示:将△ABP绕点A逆时针旋转60°,连接PP',得到△APP'是等边三角形,△PP'C是直角三角形.
将△ABP绕点A逆时针旋转60°,连接PP',PB= P'C=10
∴△APP'是等边三角形
∴PP'=6
∵PP'2+PC2= P'C2
∴△PP'C是直角三角形
∴∠APC=∠P'PC- ∠P'PA=30°
解决问题:类比前面的方法,通过旋转构造直角三角形,可求得结果为135°
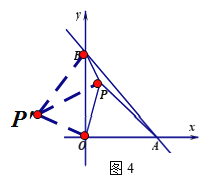
将△APO绕O逆时针旋转90°,连接PP',
因为△P’OP是等腰直角三角形,
所以PP’=![]() =2
=2![]() ,
,
因为△P’OB≌△POA,
所以P’B=PA=3.
在△P’PB中,∵PP’2+PB2=P’B2,
∴△P’PB是直角三角形,
∴∠BPP’=90°,
∴∠BPO=90°+45°=135°


科目:初中数学 来源: 题型:
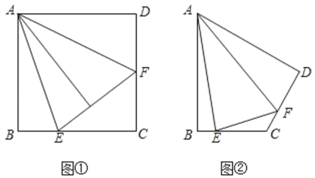
【题目】探究:如图①点E、F分别在正方形ABCD的边BC、CD上,连结AE、AF、EF,将△ABE、△ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形.若BE=2,DF=3,求AB的长;
拓展:如图②点E、F分别在四边形BACD的边BC、CD上,且∠B=∠D=90°.连结AE、AF、EF将△ABE、△ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与△AEF完全重合的三角形.若∠EAF=30°,AB=4,则△ECF的周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E,F分别是边AB,AD上的点,连接CE,CF并延长,分别交DA,BA的廷长线于点H,G.
(1)如图1,若四边形ABCD是菱形,∠ECF=![]() ∠BCD,求证:AC2=AHAG;
∠BCD,求证:AC2=AHAG;
(2)如图2,若四边形ABCD是正方形,∠ECF=45°,BC=4,设AE=x,AG=y,求y与x的函数关系式;
(3)如图3,若四边形ABCD是矩形,AB:AD=1:2,CG=CH,∠GCH=45°,请求tan∠AHG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=3cm.点P从点A出发,以每秒1cm的速度向终点B运动,同时点Q从点B出发,以每秒3cm的速度沿BC﹣CD﹣DA向终点A运动,到达各自终点时停止运动.设动点的运动时间为x秒,△PBQ的面积为ycm2,则能正确表示△PBQ的面积y与时间x的关系的图象是( )
A.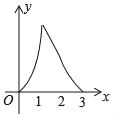 B.
B.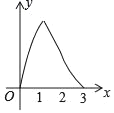
C.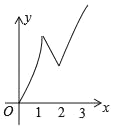 D.
D.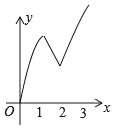
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从淄博汽车站到银泰城有甲,乙,丙三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从淄博汽车站到银泰城的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
线路/公交车用时的频数/公交车用时 | 30≤t≤35 | 35≤t≤40 | 40≤t≤45 | 45≤t≤50 | 合计 |
甲 | 59 | 151 | 166 | 124 | 500 |
乙 | 50 | 50 | 122 | 278 | 500 |
丙 | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐线路上的公交车,从淄博汽车站到银泰城“用时不超过45分钟”的可能性最大.( )
A.甲B.乙C.丙D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形![]() 中,
中,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,把四边形
,把四边形![]() 沿
沿![]() 所在直线折叠,使点
所在直线折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,点
处,点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .
.


(1)证明:![]() ;
;
(2)求四边形![]() 面积;
面积;
(3)如图2,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路径以每秒
路径以每秒![]() 的速度匀速运动,设运动时间为
的速度匀速运动,设运动时间为![]() 秒,当
秒,当![]() 为何值时,
为何值时,![]() 的面积与四边形
的面积与四边形![]() 的面积相等.
的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尺规作图:如图,![]() 、
、![]() 是平面上两个定点,在平面上找一点
是平面上两个定点,在平面上找一点![]() ,使
,使![]() 构成等腰直角三角形,且
构成等腰直角三角形,且![]() 为直角顶点.(画出一个点
为直角顶点.(画出一个点![]() 即可)
即可)

(2)在(1)的条件下,若![]() ,
,![]() ,则点
,则点![]() 的坐标是________.
的坐标是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com