
【题目】已知:△ABC内接于⊙O,CD⊥AB于点D.
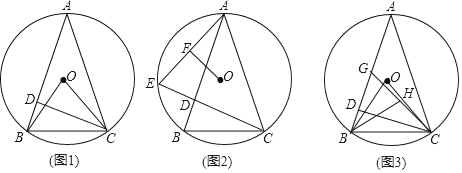
(1)如图1,连接OB和OC,AB=AC,求证:∠BOC=4∠BCD;
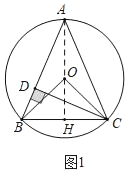
(2)如图2,延长CD交⊙O于点E,连接AE,过点O作OF⊥AE,垂足为F,求证:BC=2OF;
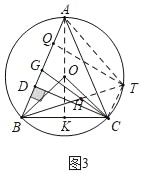
(3)如图3,在(1)的条件下,G是AB上一点,连接CG,H为CG的中点,连接BH,若∠BAC=∠HBA,AG=8,BH=9,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)如图1中,连接AO,延长AO交BC于H.首先证明∠BCD=∠BAH,再证明∠BOC=4∠BAH即可解决问题.
(2)如图2中,连接AO,延长AO交⊙O于H,连接EH,BH.利用三角形中位线定理证明EH=2OF,再证明BC=EH即可.
(3)如图3中,连接AO,延长AO交BC于K,延长BH交⊙O于T,连接CT,AT,作TQ⊥AB于Q.首先证明CT⊥AB,证明△BHG≌△THC(AAS),推出BH=TH=9,再求出BC,AK即可解决问题.
解:(1)证明:如图1中,连接AO,延长AO交BC于H.
∵AB=AC,
∴![]() ,∠ABC=∠ACB,
,∠ABC=∠ACB,
∴AH⊥BC,
∴∠BAH=∠CAH,
∵CD⊥AB,
∴∠AHB=∠CDB=90°,
∴∠CBD+∠ABC=90°,∠ABC+∠BAH=90°,
∴∠BCD=∠BAH,
∵OA=OB=OC,
∴∠OAB=∠OBA=∠OAC=∠OCA,
∵∠BOH=∠OAB+∠OBA,∠COH=∠OAC+∠OCA,
∴∠BOC=4∠OAB=4∠BCD.
(2)证明:如图2中,连接AO,延长AO交⊙O于H,连接EH,BH.

∵OF⊥AE,
∴AF=FE,
∵AO=OH,
∴EH=2OF,
∵AH是直径,
∴∠ABH=90°,
∵CD⊥AB,
∴∠ADC=∠ABH=90°,
∴EC∥BH,
∴∠ECB=∠CBH,
∴![]() ,
,
∴![]() ,
,
∴EH=BC,
∴BC=2OF.
(3)如图3中,连接AO,延长AO交BC于K,延长BH交⊙O于T,连接CT,AT,作TQ⊥AB于Q.
∵∠BTC=∠BAC,∠BAC=∠ABH,
∴∠ABH=∠BTC,
∴AB∥CT,![]() ,
,
∴![]() ,BC=AT,
,BC=AT,
∴BT=AC=AB,
∵∠BHG=∠THC,∠GBH=∠CTH,GH=HC,
∴△BHG≌△THC(AAS),
∴BH=TH=9,BG=CT,
∴AB=BT=AC=18,
∵AG=8,
∴BG=CT=10,
∵TQ⊥AB,CD⊥AB,BC=AT,易证AQ=BD=4,AD=BQ=14,
∴BC2=BD2+CD2=BD2+AC2﹣AD2=144,
∴BC=12,
在Rt△ABK中,AK=![]() =
=![]() =12
=12![]() ,
,
设OA=OB=r,
在Rt△BOK中,则有r2=62+(12![]() ﹣r)2,
﹣r)2,
∴r=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() 与y轴交于A,与x轴交于D,抛物线y=
与y轴交于A,与x轴交于D,抛物线y=![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
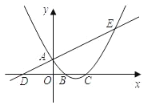
(1)求抛物线的解析式;
(2)点P是直线AE上一动点,当△PBC周长最小时,求点P坐标;
(3)动点Q在x轴上移动,当△QAE是直角三角形时,求点Q的坐标;
(4)在y轴上是否存在一点M,使得点M到C点的距离与到直线AD的距离恰好相等?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;

(2)若⊙O半径为1,求菱形ACBP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=3cm.点P从点A出发,以每秒1cm的速度向终点B运动,同时点Q从点B出发,以每秒3cm的速度沿BC﹣CD﹣DA向终点A运动,到达各自终点时停止运动.设动点的运动时间为x秒,△PBQ的面积为ycm2,则能正确表示△PBQ的面积y与时间x的关系的图象是( )
A.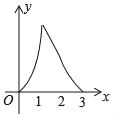 B.
B.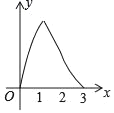
C.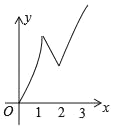 D.
D.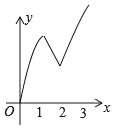
查看答案和解析>>
科目:初中数学 来源: 题型:
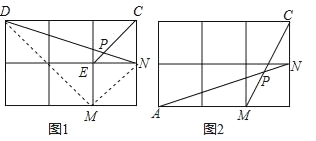
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
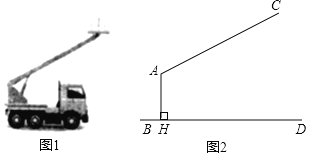
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
查看答案和解析>>
科目:初中数学 来源: 题型:
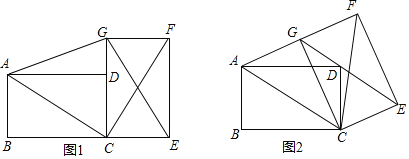
【题目】两张矩形纸片ABCD和CEFG完全相同,且AB=CE,AD>AB.
操作发现:
(1)如图1,点D在GC上,连接AC、CF、CG、AG,则AC和CF有何数量关系和位置关系?并说明理由.
实践探究:
(2)如图2,将图1中的纸片CEFG以点C为旋转中心逆时针旋转,当点D落在GE上时停止旋转,则AG和GF在同一条直线上吗?请判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC与点E,经过A、D、E三点的即的圆心F恰好在y轴上,⊙F与y轴交于另一点G.
(1)求证:BC是⊙F的切线;
(2)试探究线段AG、AD、CD之间的关系,并证明;
(3)若点A(O,﹣1)、D(2,0),求AB的长.
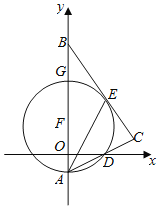
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com