
【题目】两张矩形纸片ABCD和CEFG完全相同,且AB=CE,AD>AB.
操作发现:
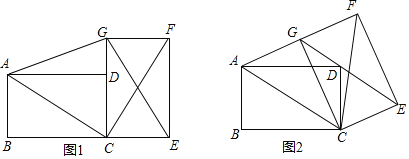
(1)如图1,点D在GC上,连接AC、CF、CG、AG,则AC和CF有何数量关系和位置关系?并说明理由.
实践探究:
(2)如图2,将图1中的纸片CEFG以点C为旋转中心逆时针旋转,当点D落在GE上时停止旋转,则AG和GF在同一条直线上吗?请判断,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析.
,理由见解析.
【解析】
(1)先根据条件判定△ABC≌△CEF,进而得到AC=CF,∠ACB=∠CFE,再根据∠CFE+∠ECF=90°,得出∠ACF=90°,即可得到AC⊥CF;
(2)先根据条件判定△ACD≌△GEC,即可得出∠ACD=∠GEC,DC=EC,AC=GE,进而判定四边形ACEG是平行四边形,得出AG∥CE,再根据矩形CEFG中,GF∥CE,即可得到AG和GF在同一条直线上.
(1)AC=CF,AC⊥CF.理由如下:
如图1,
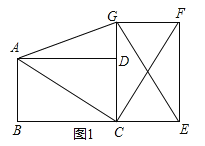
∵矩形纸片ABCD和CEFG完全相同,且AB=CE,
∴BC=EF,∠B=∠CEF=90°,
在△ABC和△CEF中,
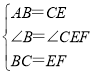 ,
,
∴△ABC≌△CEF(SAS),
∴AC=CF,∠ACB=∠CFE,
∵Rt△CEF中,∠CFE+∠ECF=90°,
∴∠ACB+∠ECF=90°,
∴∠ACF=∠BCD+∠ECG-(∠ACB+∠ECF)=90°+90°-90°=90°,
∴AC⊥CF;
(2)AG和GF在同一条直线上.理由如下:
如图2,
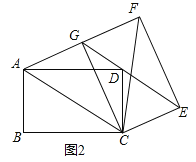
∵矩形纸片ABCD和CEFG完全相同,且AB=CE,
∴AD=GC,CD=CE,∠ADC=∠GCE=90°,
在△ACD和△GEC中,
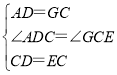 ,
,
∴△ACD≌△GEC(SAS),
∴∠ACD=∠GEC,DC=EC,AC=GE,
∴∠CDE=∠DEC,
∴∠ACD=∠CDE,
∴GE∥AC,
∴四边形ACEG是平行四边形,
∴AG∥CE,
又∵矩形CEFG中,GF∥CE,
∴AG和GF在同一条直线上.(过直线外一点有且只有一条直线与已知直线平行)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
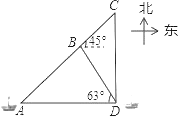
【题目】某渔船向正东方向航行,上午8点在A处时发现渔船、小岛B和小岛C在同一条直线上,渔船以30海里/小时的速度继续向正东方向航行,上午10点到达位于小岛C的正南方向上的D处,此时小岛B在渔船的西偏北63°的方向上,如图,已知小岛C在小岛B的东偏北45°的方向上,求小岛B和小岛C之间的距离.(结果精确到1海里,参考数据:sin63°≈0.9,cos63°≈0.5,tan63°≈2.0,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,CD⊥AB于点D.
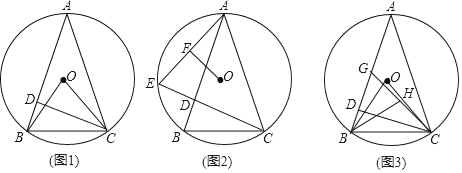
(1)如图1,连接OB和OC,AB=AC,求证:∠BOC=4∠BCD;
(2)如图2,延长CD交⊙O于点E,连接AE,过点O作OF⊥AE,垂足为F,求证:BC=2OF;
(3)如图3,在(1)的条件下,G是AB上一点,连接CG,H为CG的中点,连接BH,若∠BAC=∠HBA,AG=8,BH=9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
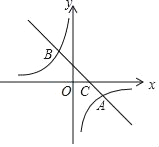
【题目】如图,在平面直角坐标系中,一次函数y=k1x+b的图象与反比例函数y=![]() 的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
的图象交于A(4,﹣2)、B(﹣2,n)两点,与x轴交于点C.
(1)求k2,n的值;
(2)请直接写出不等式k1x+b<![]() 的解集;
的解集;
(3)将x轴下方的图象沿x轴翻折,点A落在点A′处,连接A′B,A′C,求△A′BC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
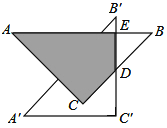
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,点D为BC边的中点,将△ABC绕点D逆时针旋转45度,得到△A′B′C′,B′C′与AB交于点E,则图中阴影部分四边形ACDE的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
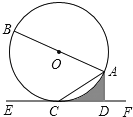
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对该市市民的购物方式进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请根据两幅统计图中提供的信息,解答下列问题:
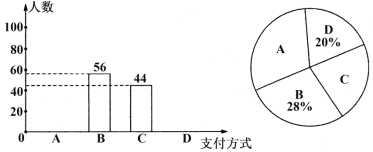
⑴求本次一共调查的购买者人数;
⑵请补全条形统计图;
⑶求在扇形统计图中A种支付方式所对应的圆心角度数;
⑷若该超市一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
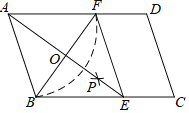
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于![]() 的长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
的长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形.
(2)设AE与BF相交于点O,四边形ABEF的周长为16,BF=4,求AE的长和∠C的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com