
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC与点E,经过A、D、E三点的即的圆心F恰好在y轴上,⊙F与y轴交于另一点G.
(1)求证:BC是⊙F的切线;
(2)试探究线段AG、AD、CD之间的关系,并证明;
(3)若点A(O,﹣1)、D(2,0),求AB的长.
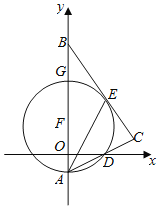
【答案】(1)详见解析;(2)AG=AD+2CD;(3)![]()
【解析】
(1)连接EF,根据角平分线的定义、等腰三角形的性质得到∠FEA=∠EAC,得到FE∥AC,根据平行线的性质得到∠FEB=∠C=90°,证明结论;
(2)作FR⊥AD于R,连接DF,得出四边形RCEF是矩形,则EF=RC=RD+CD,∠EFR=90°,得出AR=RD=![]() AD,即可得出结论;
AD,即可得出结论;
(3)设⊙F的半径为r,则r2=(r-1)2+22,解得,r=![]() ,则FA=FG=FE=
,则FA=FG=FE=![]() ,由勾股定理得出AD=
,由勾股定理得出AD=![]() ,得出AR=
,得出AR=![]() ,证明△BEF∽△FRA,得出
,证明△BEF∽△FRA,得出![]() ,求出BF
,求出BF![]() ,即可得出结果.
,即可得出结果.
(1)证明:连接EF,如图1所示:
∵AE平分∠BAC,
∴∠FAE=∠CAE,
∵FA=FE,
∴∠FAE=∠FEA,
∴∠FEA=∠EAC,
∴FE∥AC,
∴∠FEB=∠C=90°,即BC是⊙F的切线;
(2)解:AG=AD+2CD;理由如下:
作FR⊥AD于R,连接DF,如图2所示:
则∠FRC=90°,又∠FEC=∠C=90°,
∴四边形RCEF是矩形,
∴EF=RC=RD+CD,∠EFR=90°,
∵FR⊥AD,
∴AR=RD=![]() AD,
AD,
∴EF=RD+CD=![]() AD+CD,
AD+CD,
∵AF=EF,
∴AF=![]() AD+CD,
AD+CD,
∴AG=2AF=AD+2CD;
(3)解:设⊙F的半径为r,
则r2=(r﹣1)2+22,
解得,r=![]() ,
,
∴FA=FG=FE=![]() ,
,
∵点A(O,﹣1)、D(2,0),
∴OA=1,OD=2,
∴AD=![]() ,
,
∴AR=![]() ,
,
∵∠EFR=90°,
∴∠BFE+∠AFR=90°,
∵∠BFE+∠EBF=90°,
∴∠EBF=∠AFR,
∵∠BEF=∠FRA=90°,
∴△BEF∽△FRA,
∴![]() ,即
,即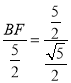 ,
,
解得:BF![]() ,
,
∴AB=AF+BF=![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:△ABC内接于⊙O,CD⊥AB于点D.
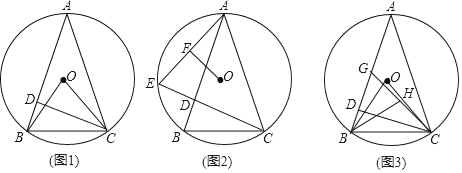
(1)如图1,连接OB和OC,AB=AC,求证:∠BOC=4∠BCD;
(2)如图2,延长CD交⊙O于点E,连接AE,过点O作OF⊥AE,垂足为F,求证:BC=2OF;
(3)如图3,在(1)的条件下,G是AB上一点,连接CG,H为CG的中点,连接BH,若∠BAC=∠HBA,AG=8,BH=9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对该市市民的购物方式进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请根据两幅统计图中提供的信息,解答下列问题:
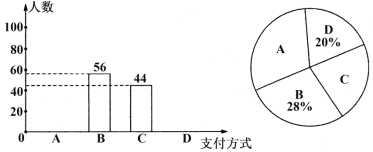
⑴求本次一共调查的购买者人数;
⑵请补全条形统计图;
⑶求在扇形统计图中A种支付方式所对应的圆心角度数;
⑷若该超市一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 | 频数 |
1.2≤x<1.6 | a |
1.6≤x<2.0 | 12 |
2.0≤x<2.4 | b |
2.4≤x<2.8 | 10 |
请根据图表中所提供的信息,完成下列问题:
(1)表中a= ,b= ,样本成绩的中位数落在 范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?
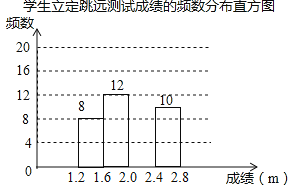
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 | 划记 | 频数 | 百分比 |
优秀 | 正正正 | a | 30% |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 15% |
不合格 |
| 3 | 5% |
合计 | 60 | 60 | 100% |
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=_____,b=_____;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为_____.
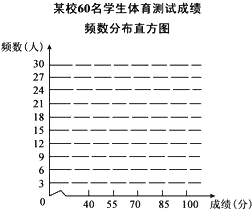
查看答案和解析>>
科目:初中数学 来源: 题型:
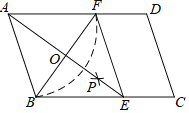
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于![]() 的长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
的长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形.
(2)设AE与BF相交于点O,四边形ABEF的周长为16,BF=4,求AE的长和∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)
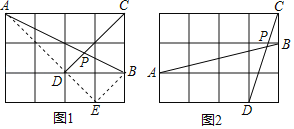
如图1,在边长为1的正方形网格中,连结格点A、B和C、D,AB和CD相交于点P,求tan∠CPB的值.小马同学是这样解决的:连结格点B、E可得BE∥CD,则∠ABE=∠CPB,连结AE,那么∠CPB就变换到Rt△ABE中.则tan∠CPB的值为 .
(探索延伸)
如图2,在边长为1的正方形网格中,AB和CD相交于点P,求sin∠APD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com