
【题目】(问题背景)
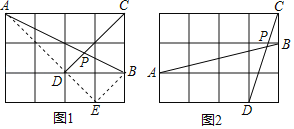
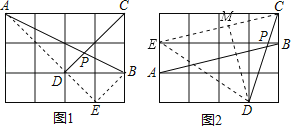
如图1,在边长为1的正方形网格中,连结格点A、B和C、D,AB和CD相交于点P,求tan∠CPB的值.小马同学是这样解决的:连结格点B、E可得BE∥CD,则∠ABE=∠CPB,连结AE,那么∠CPB就变换到Rt△ABE中.则tan∠CPB的值为 .
(探索延伸)
如图2,在边长为1的正方形网格中,AB和CD相交于点P,求sin∠APD的值.
【答案】【问题背景】3;【探索延伸】sin∠APD=![]() .
.
【解析】
(1)在Rt△ABE中,利用正切函数的定义求出tan∠ABE即可.
(2)如图2,连接CE,DE,作DM⊥CE于M.先证明四边形ABCE是平行四边形,得出CE∥AB,那么∠APD=∠ECD.利用割补法求出△ECD的面积=![]() ,由勾股定理求出CE=
,由勾股定理求出CE=![]() ,那么根据三角形的面积公式得出DM=
,那么根据三角形的面积公式得出DM=![]() ,然后利用正弦函数定义求出sin∠ECD即可.
,然后利用正弦函数定义求出sin∠ECD即可.
解:(1)如图1,
∵BE∥CD,
∴∠ABE=∠CPB,
∴tan∠ABE=tan∠CPB,
∵∠AEB=90°,
∴tan∠CPB=tan∠ABE=![]() =3,
=3,
故答案为3.
(2)如图2,连接CE,DE,作DM⊥CE于M.
∵BC∥AE,BC=AE,
∴四边形ABCE是平行四边形,
∴CE∥AB,
∴∠APD=∠ECD.
∵△ECD的面积=3×4﹣![]() ×1×4﹣
×1×4﹣![]() ×2×3﹣
×2×3﹣![]() ×1×3=
×1×3=![]() ,
,
∴![]() CEDM=
CEDM=![]() ,
,
∵CE=![]() ,
,
∴DM=![]() ,
,
∴sin∠APD=sin∠ECD=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC与点E,经过A、D、E三点的即的圆心F恰好在y轴上,⊙F与y轴交于另一点G.
(1)求证:BC是⊙F的切线;
(2)试探究线段AG、AD、CD之间的关系,并证明;
(3)若点A(O,﹣1)、D(2,0),求AB的长.
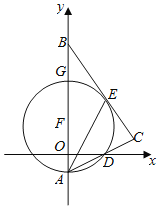
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解全国中学生最喜爱哪位歌手,适合全面调查.
B.甲乙两种麦种,连续3年的平均亩产量相同,它们的方差为:S甲2=5,S乙2=0.5,则甲麦种产量比较稳.
C.某次朗读比赛中预设半数晋级,某同学想知道自己是否晋级,除知道自己的成绩外,还需要知道平均成绩.
D.一组数据:3,2,5,5,4,6的众数是5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数![]() (k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )
(k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )
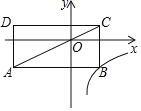
A.![]() B.
B.![]() C.4D.﹣4
C.4D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国明代著名数学家程大位的《算法统宗》一书中记载了一些诗歌形式的算题,其中有一个“百羊问题”:甲赶群羊逐草茂,乙拽肥羊一只随其后;戏问甲及一百否?甲云所说无差谬,若得这般一群凑,再添半群小半群,得你一只来方凑.玄机奥妙谁猜透.题目的意思是:甲赶了一群羊在草地上往前走,乙牵了一只肥羊紧跟在甲的后面.乙问甲:“你这群羊有一百只吗?”甲说:“如果再有这么一群,再加半群,又加四分之一群,再把你的一只凑进来,才满100只.”请问甲原来赶的羊一共有多少只?如果设甲原来赶的羊一共有![]() 只,那么可列方程为______________.
只,那么可列方程为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
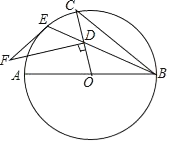
【题目】如图,AB是⊙O的直径,BE是弦,点D是弦BE上一点,连接OD并延长交⊙O于点C,连接BC,过点D作FD⊥OC交⊙O的切线EF于点F.
(1)求证:∠CBE=![]() ∠F;
∠F;
(2)若⊙O的半径是2![]() ,点D是OC中点,∠CBE=15°,求线段EF的长.
,点D是OC中点,∠CBE=15°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△PAD的面积为( )
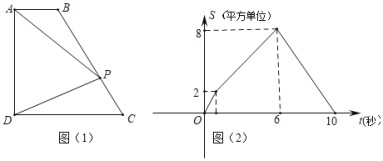
A. 4B. 5C. 6D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com