
【题目】如图,在正方形ABCD中,E,F分别是边BC、CD上的点,BE=CF,AF与DE相交于点O,CG⊥DE,垂足为G.,求证:AD![]() =AOAF;
=AOAF;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
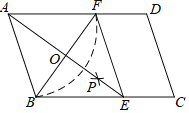
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B,F为圆心,大于![]() 的长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
的长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形.
(2)设AE与BF相交于点O,四边形ABEF的周长为16,BF=4,求AE的长和∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是半圆O上一个动点,AB为半圆的直径,D是弧BC的中点,过点D作半圆O的切线DE交AC的延长线于点E.
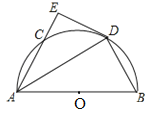
(1)求证:AE⊥DE;
(2)①已知CE=2,DE=4,则AB= ;
②连接OC,DC,当∠BAC= 度时,四边形OBDC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
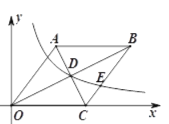
【题目】如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).
(1)请求出菱形的边长;
(2)若反比例函数![]() 经过菱形对角线的交点D,且与边BC交于点E,请求出点E的坐标.
经过菱形对角线的交点D,且与边BC交于点E,请求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)
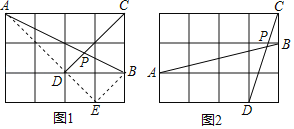
如图1,在边长为1的正方形网格中,连结格点A、B和C、D,AB和CD相交于点P,求tan∠CPB的值.小马同学是这样解决的:连结格点B、E可得BE∥CD,则∠ABE=∠CPB,连结AE,那么∠CPB就变换到Rt△ABE中.则tan∠CPB的值为 .
(探索延伸)
如图2,在边长为1的正方形网格中,AB和CD相交于点P,求sin∠APD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为DC、DA边上的点,∠EBF=45°,若EF=5,CE=2,则正方形ABCD的边长为( )

A.8B.6C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com