
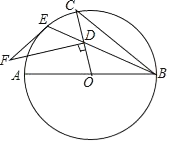
【题目】如图,AB是⊙O的直径,BE是弦,点D是弦BE上一点,连接OD并延长交⊙O于点C,连接BC,过点D作FD⊥OC交⊙O的切线EF于点F.
(1)求证:∠CBE=![]() ∠F;
∠F;
(2)若⊙O的半径是2![]() ,点D是OC中点,∠CBE=15°,求线段EF的长.
,点D是OC中点,∠CBE=15°,求线段EF的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OE交DF于点H,由切线的性质得出∠F+∠EHF =90,由FD⊥OC得出∠DOH+∠DHO =90,依据对顶角的定义得出∠EHF=∠DHO,从而求得∠F=∠DOH,依据∠CBE=![]() ∠DOH,从而即可得证;
∠DOH,从而即可得证;
(2)依据圆周角定理及其推论得出∠F=∠COE=2∠CBE =30°,求出OD的值,利用锐角三角函数的定义求出OH的值,进一步求得HE的值,利用锐角三角函数的定义进一步求得EF的值.
(1)证明:连接OE交DF于点H,
∵EF是⊙O的切线,OE是⊙O的半径,
∴OE⊥EF.
∴∠F+∠EHF=90°.
∵FD⊥OC,
∴∠DOH+∠DHO=90°.
∵∠EHF=∠DHO,
∴∠F=∠DOH.
∵∠CBE=![]() ∠DOH,
∠DOH,
∴![]()
(2)解:∵∠CBE=15°,
∴∠F=∠COE=2∠CBE=30°.
∵⊙O的半径是![]() ,点D是OC中点,
,点D是OC中点,
∴![]() .
.
在Rt△ODH中,cos∠DOH=![]() ,
,
∴OH=2.
∴![]() .
.
在Rt△FEH中,![]()
∴![]()


科目:初中数学 来源: 题型:
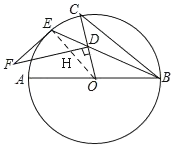
【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 | 划记 | 频数 | 百分比 |
优秀 | 正正正 | a | 30% |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 15% |
不合格 |
| 3 | 5% |
合计 | 60 | 60 | 100% |
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=_____,b=_____;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)
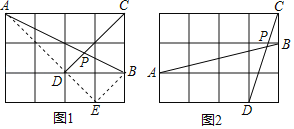
如图1,在边长为1的正方形网格中,连结格点A、B和C、D,AB和CD相交于点P,求tan∠CPB的值.小马同学是这样解决的:连结格点B、E可得BE∥CD,则∠ABE=∠CPB,连结AE,那么∠CPB就变换到Rt△ABE中.则tan∠CPB的值为 .
(探索延伸)
如图2,在边长为1的正方形网格中,AB和CD相交于点P,求sin∠APD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.根据准外心的定义,探究如下问题:如图,在RtΔABC中,∠C=90°,AB=10,AC=6,如果准外心P在BC边上,那么PC的长为 ________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车制造公司计划生产A、B两种新型汽车共40辆投放到市场销售.已知A型汽车每辆成本34万元,售价39万元;B型汽车每辆成本42万元,售价50万元.若该公司对此项计划的投资不低于1536万元,不高于1552万元.请解答下列问题:
(1)该公司有哪几种生产方案?
(2)该公司按照哪种方案生产汽车,才能在这批汽车全部售出后,所获利润最大,最大利润是多少?
(3)在(2)的情况下,公司决定拿出利润的2.5%全部用于生产甲乙两种钢板(两种都生产),甲钢板每吨5000元,乙钢板每吨6000元,共有多少种生产方案?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3名学生各自随机选择到A、B两个书店购书.
(1)则甲、乙2名学生在不同书店购书的概率是________;
(2)求甲、乙、丙3名学生在同一书店购书的概率.
(请用画“树状图”或“列表”等方法写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
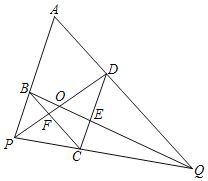
【题目】如图, 已知菱形![]() ,
,![]() ,点
,点![]() 是边
是边![]() 延长线上一点, 连接
延长线上一点, 连接![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式, 并写出它的定义域;
的函数解析式, 并写出它的定义域;
(3)当![]() 与
与![]() 相似时, 求
相似时, 求![]() 的值 .
的值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com