
【题目】某汽车制造公司计划生产A、B两种新型汽车共40辆投放到市场销售.已知A型汽车每辆成本34万元,售价39万元;B型汽车每辆成本42万元,售价50万元.若该公司对此项计划的投资不低于1536万元,不高于1552万元.请解答下列问题:
(1)该公司有哪几种生产方案?
(2)该公司按照哪种方案生产汽车,才能在这批汽车全部售出后,所获利润最大,最大利润是多少?
(3)在(2)的情况下,公司决定拿出利润的2.5%全部用于生产甲乙两种钢板(两种都生产),甲钢板每吨5000元,乙钢板每吨6000元,共有多少种生产方案?(直接写出答案)
【答案】(1)共有三种方案,分别为①A型号16辆时, B型号24辆;②A型号17辆时,B型号23辆;③A型号18辆时,B型号22辆;(2)当![]() 时,
时,![]() 万元;(3)A型号4辆,B型号8辆; A型号10辆,B型号 3辆两种方案
万元;(3)A型号4辆,B型号8辆; A型号10辆,B型号 3辆两种方案
【解析】
(1)设A型号的轿车为x辆,可根据题意列出不等式组,根据问题的实际意义推出整数值;
(2)根据“利润=售价-成本”列出一次函数的解析式解答;
(3)根据(2)中方案设计计算.
(1)设生产A型号x辆,则B型号(40-x)辆
1536![]() 34x+42(40-x)
34x+42(40-x)![]() 1552
1552
解得![]() ,x可以取值16,17,18共有三种方案,分别为
,x可以取值16,17,18共有三种方案,分别为
A型号16辆时, B型号24辆
A型号17辆时,B型号23辆
A型号18辆时,B型号22辆
(2)设总利润W万元
则W=![]()
=![]()
![]()
![]() w随x的增大而减小
w随x的增大而减小
当![]() 时,
时,![]() 万元
万元
(3)A型号4辆,B型号8辆; A型号10辆,B型号 3辆两种方案


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
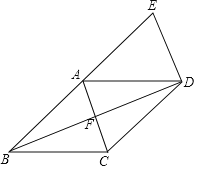
【题目】已知:四边形ACDE为平行四边形,延长EA至点B,使EA=BA,连接BD交AC于点F,连接BC
(1)求证:AD=BC.
(2)若BD=DE,当∠E= °时,四边形ABCD为正方形请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
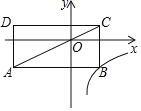
【题目】如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数![]() (k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )
(k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )
A.![]() B.
B.![]() C.4D.﹣4
C.4D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
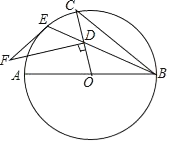
【题目】如图,AB是⊙O的直径,BE是弦,点D是弦BE上一点,连接OD并延长交⊙O于点C,连接BC,过点D作FD⊥OC交⊙O的切线EF于点F.
(1)求证:∠CBE=![]() ∠F;
∠F;
(2)若⊙O的半径是2![]() ,点D是OC中点,∠CBE=15°,求线段EF的长.
,点D是OC中点,∠CBE=15°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
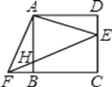
【题目】如图,△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,有如下五个结论①AE⊥AF;②EF:AF=![]() :1;③AF2=FHFE;④∠AFE=∠DAE+∠CFE ⑤ FB:FC=HB:EC.则正确的结论有( )
:1;③AF2=FHFE;④∠AFE=∠DAE+∠CFE ⑤ FB:FC=HB:EC.则正确的结论有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.

1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有三只大小、质地都相同的小球,球面上分别标有数字1、﹣2、3,搅匀后先从中任意摸出一个小球(不放回),记下数字作为点A的横坐标,再从余下的两个小球中任意摸出一个小球,记下数字作为点A的纵坐标.
(1)用画树状图或列表等方法列出所有可能出现的结果;
(2)求点A落在第四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com