
【题目】如图,四边形ABCD内接于以AC为直径的⊙O,AD=![]() ,CD=2
,CD=2![]() ,BC=BA,AC与BD相交于点F,将△ABF沿AB翻折,得到△ABG,连接CG交AB于E,则BE长为_____.
,BC=BA,AC与BD相交于点F,将△ABF沿AB翻折,得到△ABG,连接CG交AB于E,则BE长为_____.
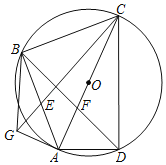
【答案】![]()
【解析】
根据圆周角定理得到∠ADC=∠ABC=90°,根据勾股定理得到![]() ,根据角平分线的性质得到FM=FN,求得
,根据角平分线的性质得到FM=FN,求得![]() ,根据折叠的性质得到∠GAE=∠CAE,得到
,根据折叠的性质得到∠GAE=∠CAE,得到![]() ,求得CG=
,求得CG=![]() ,过A作AH⊥EG于H,根据三角函数的定义得到EH=EG﹣HG=
,过A作AH⊥EG于H,根据三角函数的定义得到EH=EG﹣HG=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
解:∵AC为⊙O的直径,
∴∠ADC=∠ABC=90°,
∵AD=![]() ,CD=2
,CD=2![]() ,
,
∴![]() ,
,
∵AB=BC,
∴∠1=∠2,
过F作FM⊥AD于M,FN⊥CD于N,
∴FM=FN,
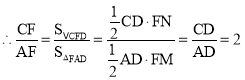 ,
,
∴![]() ,
,
∵将△ABF沿AB翻折,得到△ABG,
∴∠GAE=∠CAE,
∴![]() =3,
=3,
∵AG=AF=![]() ,
,
∵∠BAG=∠BAC=45°,
∴∠GAC=90°,
∴CG=![]() ,
,
∴![]() ,
,
过A作AH⊥EG于H,
∴HG=AGcos∠AGH=![]() ,
,
∴EH=EG﹣HG=![]() ,
,
∴AE=![]() ,
,
![]() ,
,
∴BE=AB﹣AE=![]() .
.
故答案为:![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等著名景点,该市旅游部门统计绘制出2019年“五·一”长假期间旅游情况统计图,根据以下信息解答下列问题:
等著名景点,该市旅游部门统计绘制出2019年“五·一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)扇形统计图中![]() 景点所对应的圆心角的度数是______;
景点所对应的圆心角的度数是______;
(2)请补全条形统计图和扇形统计图;
(3)根据近几年到该市旅游人数增长趋势,预计2020年“五·一”节将有80万游客选择该市旅游,请估计有多少万人会选择去![]() 景点旅游?
景点旅游?
(4)甲,乙两个旅行团在![]() ,
,![]() ,
,![]() 三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明.
三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学计划为新生配备如图(1)所示的折叠椅.图(2)是折叠椅撑开后的侧面示意图,其中椅腿AB和CD的长相等,O是它们的中点.为使折叠椅既舒适又牢固,厂家将撑开后的折叠椅高度设计为32cm,∠DOB=100°,那么椅腿的长AB和篷布面的宽AD各应设计为多少cm?(结果精确到0.1cm)
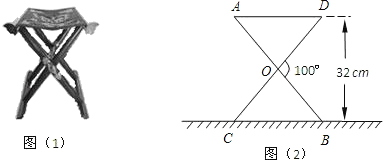
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点和点O都在正方形网格的格点上,每个小正方形的边长都为1.
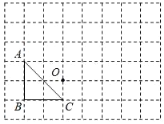
(1)将△ABC先向右平移4个单位,再向上平移2个单位得到△A1B1C1,请画出△A1B1C1;
(2)请画出△A2B2C2,使△A2B2C2和△ABC关于点O成中心对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() 与y轴交于A,与x轴交于D,抛物线y=
与y轴交于A,与x轴交于D,抛物线y=![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为 (1,0).
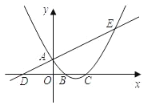
(1)求抛物线的解析式;
(2)点P是直线AE上一动点,当△PBC周长最小时,求点P坐标;
(3)动点Q在x轴上移动,当△QAE是直角三角形时,求点Q的坐标;
(4)在y轴上是否存在一点M,使得点M到C点的距离与到直线AD的距离恰好相等?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
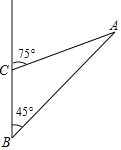
【题目】成都市第十三次党代会提出实施“东进”战略,推动了城市发展格局“千年之变”成都龙泉山城市森林公园借“东进”之风,聚全市之力,着力打造一个令世界向往的城市中心,如图为成都市龙泉山城市豪林公园三个景点A,B,C的平面示意图,景点C在B的正北方向5千米处,景点A在B的东北方向,在C的北偏东75°方向上.
(1)∠BAC的大小
(2)求景点A,C的距离(![]() =1.414,
=1.414,![]() =1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,结果精确到0.1)
=1.732,sin75°≈0.966,cos75°≈0.259,tan75°≈3.732,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;

(2)若⊙O半径为1,求菱形ACBP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
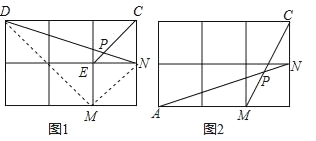
【题目】(问题呈现)如图1,在边长为1的正方形网格中,连接格点D,N和E,C,DN和EC相交于点P,求tan∠CPN的值.
(方法归纳)求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
(问题解决)(1)直接写出图1中tan∠CPN的值为 ;
(2)如图2,在边长为1的正方形网格中,AN与CM相交于点P,求cos∠CPN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商销售一种成本价为10元/kg的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不得高于18元/kg.在销售过程中发现销量y(kg)与售价x(元/kg)之间满足一次函数关系,对应关系如下表所示:
x | 12 | 14 | 15 | 17 |
y | 36 | 32 | 30 | 26 |
⑴求y与x之间的函数关系式,并写出自变量x的取值范围;
⑵若该经销商想使这种商品获得平均每天168元的利润,求售价应定为多少元/kg?
⑶设销售这种商品每天所获得的利润为W元,求W与x之间的函数关系式;并求出该商品销售单价定为多少元时,才能使经销商所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com