
 如图,抛物线y=ax2+bx(a>0)与双曲线y=
如图,抛物线y=ax2+bx(a>0)与双曲线y= 相交于点A,B.已知点A的坐标为(1,4),点B在第三象限内,连结AB交y轴于点E,且S△BOE=
相交于点A,B.已知点A的坐标为(1,4),点B在第三象限内,连结AB交y轴于点E,且S△BOE= S△AOB(O为坐标原点).
S△AOB(O为坐标原点). 上,得k=4
上,得k=4 S△AOB,
S△AOB, 上,
上,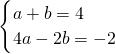
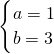
 或
或 时,
时, ,S△BOC=8
,S△BOC=8 <8
<8
 <t<-2
<t<-2 或-
或- <t<-2
<t<-2 ,S△BOC=8,得到3<
,S△BOC=8,得到3< <8,从而求得t的取值范围;
<8,从而求得t的取值范围;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 9 |
| 8 |
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?查看答案和解析>>
科目:初中数学 来源: 题型:
 O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1.查看答案和解析>>
科目:初中数学 来源: 题型:
 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,查看答案和解析>>
科目:初中数学 来源: 题型:
 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com