
【题目】如图,将一块斜边长为12cm,∠B=60°的直角三角板ABC,绕点C沿逆时针方向旋转90°至△A′B′C′的位置,再沿CB向右平移,使点B′刚好落在斜边AB上,那么此三角板向右平移的距离是cm. 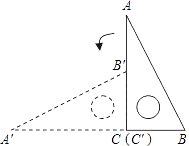
【答案】( ![]() )
)
【解析】解:如图, 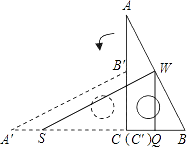
BC=ABcos60°=6.
由平移的性质知:
∠WQS=∠ACB=90°,WQ=BC=6,
∴BQ=WQcot60°=2 ![]() .
.
∴QC=BC﹣BQ=6﹣2 ![]() .
.
【考点精析】解答此题的关键在于理解平移的性质的相关知识,掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】小明在光明广场(点O)绘制了市内几所学校相对于广场的位置简图(图11中1 cm表示5 km).东方红中学在广场的正南方向,测得OA=1.7 cm,OB=2 cm,OC=2 cm,OD=1.4 cm,∠AOC=123°18′,∠AOB=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?
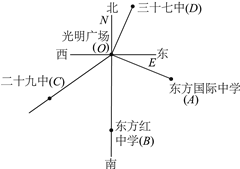
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,且位于x轴下方.
(1)若P(1,﹣3)、B(4,0),
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
(2)如图2,在(1)中的抛物线解析式不变的条件下,已知直线PA、PB与y轴分别交于E、F两点,点点P运动时,OE+OF是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( ) 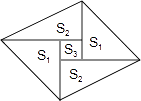
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3
查看答案和解析>>
科目:初中数学 来源: 题型:
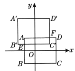
【题目】如图,长方形ABCD各顶点分别为A(-2,2),B(-2,-1),C(3,-1),D(3,2),如果长方A'B'C'D'先向右平移1个单位长度,再向下平移2个单位长度,恰能与长方形ABCD完全重合.
(1)求长方形A'B'C'D'各顶点的坐标;
(2)如果线段AB与线段B'C'交于点E,线段AD与线段C'D'交于点F,求点E,F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:

(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求出在整个平移过程中,△ABC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n-2)×180°.
(1)甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了360°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com