
【题目】直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=0.5,OB=4,OE=2. 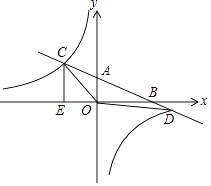
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
【答案】
(1)解:在Rt△AOB中,∵tan∠ABO=0.5,OB=4,
∴OA=2,
∴A(0,2),B(4,0),设直线AB的解析式为y=kx+b,则有 ![]() ,解得
,解得 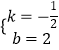 ,
,
∴直线AB的解析式为y=﹣ ![]() x+2,
x+2,
∵OE=2,CE⊥x轴,
∴C(﹣2,3),设反比例函数的解析式为y= ![]() ,
,
∴k=﹣6,
∴直线AB和反比例函数的解析式分别为y=﹣ ![]() x+2,y=﹣
x+2,y=﹣ ![]() .
.
(2)解:由 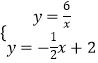 解得
解得 ![]() 或
或 ![]() ,
,
∴D(6,﹣1),
∴S△COD=S△AOC+S△AOD= ![]() ×2×2+
×2×2+ ![]() ×2×6=8.
×2×6=8.
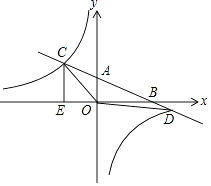
【解析】(1)在Rt△AOB中,由tan∠ABO=0.5,OB=4,推出OA=2,推出A(0,2),B(4,0),设直线AB的解析式为y=kx+b,利用待定系数法即可解决问题.(2)利用方程组求出点D坐标,根据S△COD=S△AOC+S△AOD计算即可.
【考点精析】关于本题考查的解直角三角形,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知,一条直线经过点A(1,3)和B(2,5).求:
(1)这个一次函数的解析式.
(2)当x=﹣3时,y的值.
(3)求此一次函数与x轴、y轴的交点坐标及其图像与两坐标轴围成的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·西宁)(本小题满分7分)给出三个整式a2,b2和2ab.
(1)当a=3,b=4时,求a2+b2+2ab的值;
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解.请写也你所选的式子及因式分解的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( ) 
A.x<﹣1
B.x>2
C.﹣1<x<0,或x>2
D.x<﹣1,或0<x<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线的对称轴为x=﹣1,与x轴交于A,B两点,与y轴交于点C,其中A(﹣3,0)、C(0,﹣2).
(1)求这条抛物线的函数表达式.
(2)已知在对称轴上存在一点P,使得△PBC的周长最小.请求出点P的坐标. 
(3)若点D是线段OC上的一个动点(不与点O、点C重合).过点D作DE∥PC交x轴于点E.连接PD、PE.设CD的长为m,△PDE的面积为S.求S与m之间的函数关系式.试说明S是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( ) 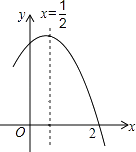
A.①②④
B.③④
C.①③④
D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com