
【题目】已知关于x的方程![]() 有两个正整数根
有两个正整数根![]() 是正整数
是正整数![]() 的三边a、b、c满足
的三边a、b、c满足![]() ,
,![]() ,
,![]() .
.
求:![]() 的值;
的值;
![]() 的面积.
的面积.
【答案】![]() m=2
m=2![]() 1或
1或![]()
【解析】
(1)本题可先求出方程(m2-1)x2-3(3m-1)x+18=0的两个根,然后根据这两个根都是正整数求出m的值.
(2)由(1)得出的m的值,然后将m2+a2m-8a=0,m2+b2m-8b=0.进行化简,得出a,b的值.然后再根据三角形三边的关系来确定符合条件的a,b的值,进而得出三角形的面积.
![]() 关于x的方程
关于x的方程![]() 有两个正整数根
有两个正整数根![]() 是整数
是整数![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,![]() 是此方程的两个根,
是此方程的两个根,
![]() ,
,
![]() 也是正整数,即
也是正整数,即![]() 或2或3或6或9或18,
或2或3或6或9或18,
又m为正整数,
![]() ;
;
![]() 把
把![]() 代入两等式,化简得
代入两等式,化简得![]() ,
,![]()
当![]() 时,
时,![]()
当![]() 时,a、b是方程
时,a、b是方程![]() 的两根,而
的两根,而![]() ,由韦达定理得
,由韦达定理得![]() ,
,![]() ,则
,则![]() 、
、![]() .
.
![]() ,
,![]() 时,由于
时,由于![]()
故![]() 为直角三角形,且
为直角三角形,且![]() ,
,![]() .
.
![]() ,
,![]() 时,因
时,因![]() ,故不能构成三角形,不合题意,舍去.
,故不能构成三角形,不合题意,舍去.
![]() ,
,![]() 时,因
时,因![]() ,故能构成三角形.
,故能构成三角形.
![]()
综上,![]() 的面积为1或
的面积为1或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分10分)某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
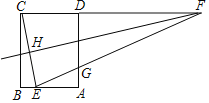
【题目】如图,矩形ABCD中,AB=3,AD=4,E在AB上,AE=2,HF是CE的垂直平分线,交CD的延长线于点F,连结EF交AD于点G,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=5,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为2的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作s1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作s2.照此规律作下去,则s2019=_____.
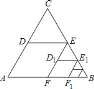
查看答案和解析>>
科目:初中数学 来源: 题型:
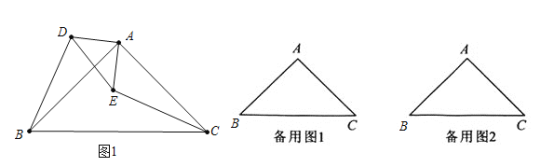
【题目】如图,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,把
,把![]() 绕点A旋转.
绕点A旋转.
![]() 当
当![]() 时,求PB的长;
时,求PB的长;
![]() 直接写出旋转过程中线段PB长的最大值与最小值.
直接写出旋转过程中线段PB长的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … | -3 | 1 | 3 | 1 | … |
则下列判断中正确的是( )
A.抛物线开口向上B.抛物线与![]() 轴的交点在
轴的交点在![]() 轴负半轴上
轴负半轴上
C.当![]() 时,
时,![]() D.方程
D.方程![]() 的正根在3与4之间
的正根在3与4之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线与x轴的两个交点及其顶点构成等边三角形,则称该抛物线“等边抛物线”.
(1)若对任意m,n,点M(m,n)和点N(-m+4,n)恒在“等边抛物线”![]() :
:![]() 上,求抛物线
上,求抛物线![]() 的解析式;
的解析式;
(2)若抛物线![]() :
:![]() “等边抛物线”,求
“等边抛物线”,求![]() 的值;
的值;
(3)对于“等边抛物线”![]() :
:![]() ,当1<x<m吋,总存在实数b。使二次函数
,当1<x<m吋,总存在实数b。使二次函数![]() 的图象在一次函数y=x图象的下方,求m的最大值.
的图象在一次函数y=x图象的下方,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A. 众数是7 B. 中位数是6.5
C. 平均数是 6.5 D. 平均每周锻炼超过6小时的人占总数的一半
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com