
【题目】若抛物线与x轴的两个交点及其顶点构成等边三角形,则称该抛物线“等边抛物线”.
(1)若对任意m,n,点M(m,n)和点N(-m+4,n)恒在“等边抛物线”![]() :
:![]() 上,求抛物线
上,求抛物线![]() 的解析式;
的解析式;
(2)若抛物线![]() :
:![]() “等边抛物线”,求
“等边抛物线”,求![]() 的值;
的值;
(3)对于“等边抛物线”![]() :
:![]() ,当1<x<m吋,总存在实数b。使二次函数
,当1<x<m吋,总存在实数b。使二次函数![]() 的图象在一次函数y=x图象的下方,求m的最大值.
的图象在一次函数y=x图象的下方,求m的最大值.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)m的最大值为6.
;(3)m的最大值为6.
【解析】
(1)先由点M和点N关于对称轴对称,可得对称轴x=2,依据x=![]() ,可得b=-4a,从而得
,可得b=-4a,从而得![]() ,然后分a>0和a<0两种情况讨论,根据等边三角形性质得出顶点坐标,代入计算即可;
,然后分a>0和a<0两种情况讨论,根据等边三角形性质得出顶点坐标,代入计算即可;
(2)设等边抛物线与x轴的两个交点分别为![]() ,
,![]() ,知
,知![]() ,结合顶点坐标
,结合顶点坐标![]() ,可得:
,可得: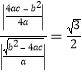 ,由此即可求出
,由此即可求出![]() ;
;
(3)由(2)中![]() 可得
可得![]() ,结合该等边抛物线过(1,1),求得b=-6或b=2,依据对称轴位置可知b=-6,联立
,结合该等边抛物线过(1,1),求得b=-6或b=2,依据对称轴位置可知b=-6,联立![]() ,解得x=1或x=6,从而得出答案.
,解得x=1或x=6,从而得出答案.
解:(1)由题意得,点M和点N关于对称轴对称,
∴对称轴x=![]() ,
,
∴x=![]() ,
,
∴b=-4a,
∴![]() ,
,
①当a>0时,顶点坐标为(2,-2![]() ),
),
代入![]() ,得-2
,得-2![]() =4a-8a,
=4a-8a,
解得:a=![]() ,
,
∴![]() ;
;
②当a<0时,顶点坐标为(2,2![]() ),
),
代入![]() ,得2
,得2![]() =4a-8a,
=4a-8a,
解得:a=![]() ,
,
∴![]() ;
;
综上,![]() 或
或![]() ;
;
(2)设等边抛物线与x轴的两个交点分别为![]() ,
,![]() ,
,
令![]() ,∴
,∴![]() ,
,
∴![]() ,
,
又∵抛物线顶点坐标为![]() ,
,
∴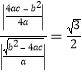 ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]()
(3)由(2)得![]() ,∴
,∴![]() ,
,
∴![]() :
:![]() ,
,
由题意可得该等边抛物线过(1,1),
∴![]() ,
,
解得:b=-6或b=2,
又对称轴x=![]() ,
,
∴b<-2,
∴b=-6,
∴![]() ,
,
联立![]() ,
,
解得x=1或x=6,
∴m的最大值为6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
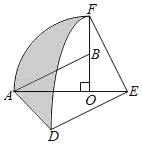
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分別以O、E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件若千元的价格购进一批商品,当每件商品售价为360元时,每月可售出100件,每件获利20%. 为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价5元,那么商场每月就可以多售出15件.
(1)该商品每件的进价是多少元?
(2)要使商场每月销售这种商品的利润达到6400元,且更有利于减少库存,则每件商品应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了一部分学生进行“风味泰兴﹣﹣我最喜爱的泰兴美食”调查活动,将调查问卷整理后绘制成如下图所示的不完整的条形统计图和扇形统计图.
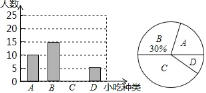
调查问卷在下面四种泰兴美食中,你最喜爱的是( )(单选)
A.黄桥烧饼 B.宣堡小馄饨C.蟹黄汤包 D.刘陈猪四宝
请根据所给信息解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图,并计算扇形统计图中“A”部分所对应的圆心角的度数为 ;
(3)若全校有1200名学生,请估计全校学生中最喜爱“蟹黄汤包”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为正方形ABCD对角线上一点,以点O为圆心,OA长为半径的
⊙ O与BC相切于点E.
(1)求证:CD是⊙ O的切线;
(2)若正方形ABCD的边长为10,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级准备购买一些奖品奖励春季运动会表现突出的同学,奖品分为甲、乙两种,已知,购买一个甲奖品比一个乙奖品多用20元,若用400元购买甲奖品的个数是用160元购买乙奖品个数的一半.
(1)求购买一个甲奖品和一个乙奖品各需多少元?
(2)经商谈,商店决定给予该班级每购买甲奖品3个就赠送一个乙奖品的优惠,如果该班级需要乙奖品的个数是甲奖品的2倍还多8个,且该班级购买两种奖项的总费用不超过640元,那么该班级最多可购买多少个甲奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
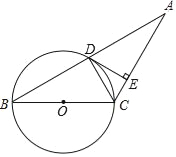
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过点D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接DC,若BC=4,求弧DC与弦DC所围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的内接三角形,
的内接三角形,![]() 为
为![]() 的直径,
的直径,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 的切线,交
的切线,交![]() 的延长线于
的延长线于![]() .
.
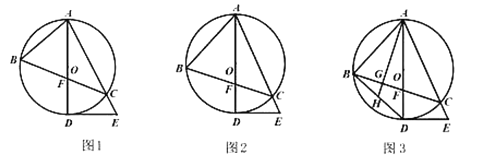
(1)求证:![]() ;
;
(2)如图,若![]() ,求证:
,求证:![]() ;
;
(3)如图,在(2)的条件下,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的中点,若
的中点,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com