
【题目】某数学兴趣小组在全校范围内随机抽取了一部分学生进行“风味泰兴﹣﹣我最喜爱的泰兴美食”调查活动,将调查问卷整理后绘制成如下图所示的不完整的条形统计图和扇形统计图.
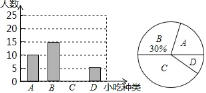
调查问卷在下面四种泰兴美食中,你最喜爱的是( )(单选)
A.黄桥烧饼 B.宣堡小馄饨C.蟹黄汤包 D.刘陈猪四宝
请根据所给信息解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图,并计算扇形统计图中“A”部分所对应的圆心角的度数为 ;
(3)若全校有1200名学生,请估计全校学生中最喜爱“蟹黄汤包”的学生有多少人?
【答案】(1)50;(2)72°;(3)480(人).
【解析】
(1)用B种小吃的人数除以对应百分比可得样本容量;
(2)根据四种小吃的人数之和等于总人数求得C的人数,据此可补全条形图,用360°乘以A部分人数占总人数的比例可得;
(3)用总人数乘以样本中C种类人数占被调查人数的比例即可得.
(1)本次抽样调查的样本容量是15÷30%=50,
故答案为:50;
(2)C种小吃的人数为50﹣(10+15+5)=20(人),
补全条形图如下:
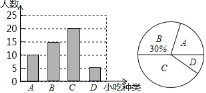
扇形统计图中“A”部分所对应的圆心角的度数为360°×![]() =72°,
=72°,
故答案为:72°;
(3)估计全校学生中最喜爱“蟹黄汤包”的学生有1200×![]() =480(人).
=480(人).


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】若数a使关于x的分式方程![]() 的解为正数,使关于y的不等式组
的解为正数,使关于y的不等式组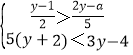 无解,则所有满足条件的整数a的值之积是( )
无解,则所有满足条件的整数a的值之积是( )
A. 360 B. 90 C. 60 D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
课题 | 测量校内旗杆高度 | ||
目的 | 运用所学数学知识及数学方法解决实际问题﹣﹣﹣测量旗杆高度 | ||
方案 | 方案一 | 方案二 | 方案三 |
示意图 |
|
| |
测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
计算过程(结 果保留根号) | 解: | 解: | |
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
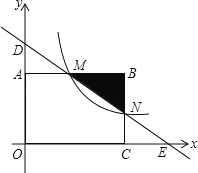
【题目】如图,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,B(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)直接写出直线DE的解析式_________;
(2)若反比例函数y=![]() (x>0)的图象与直线MN有且只有一个公共点,求m的值.
(x>0)的图象与直线MN有且只有一个公共点,求m的值.
(3)在分别过M,B的双曲线y=![]() (x>0)上是否分别存在点F,G使得B,M,F,G构成平行四边形,若存在则求出F点坐标, 若不存在则说明理由.
(x>0)上是否分别存在点F,G使得B,M,F,G构成平行四边形,若存在则求出F点坐标, 若不存在则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
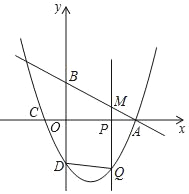
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
x+2分别交x轴、y轴于点A、B.点C的坐标是(﹣1,0),抛物线y=ax2+bx﹣2经过A、C两点且交y轴于点D.点P为x轴上一点,过点P作x轴的垂线交直线AB于点M,交抛物线于点Q,连结DQ,设点P的横坐标为m(m≠0).
(1)求点A的坐标.
(2)求抛物线的表达式.
(3)当以B、D、Q,M为顶点的四边形是平行四边形时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线与x轴的两个交点及其顶点构成等边三角形,则称该抛物线“等边抛物线”.
(1)若对任意m,n,点M(m,n)和点N(-m+4,n)恒在“等边抛物线”![]() :
:![]() 上,求抛物线
上,求抛物线![]() 的解析式;
的解析式;
(2)若抛物线![]() :
:![]() “等边抛物线”,求
“等边抛物线”,求![]() 的值;
的值;
(3)对于“等边抛物线”![]() :
:![]() ,当1<x<m吋,总存在实数b。使二次函数
,当1<x<m吋,总存在实数b。使二次函数![]() 的图象在一次函数y=x图象的下方,求m的最大值.
的图象在一次函数y=x图象的下方,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
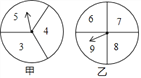
(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,从甲、乙两个大棚各收集了 24 株秧苗上的小西红柿的个数,并对数据进行整理、描述和分析。
下面给出了部分信息:(说明:45 个以下为产量不合格,45 个及以上为产量合格,其中 45~65 个为产量良好,65~85 个为产量优秀)
a.补全下面乙组数据的频数分布直方图(数据分成 6 组: 25≤x<35,35≤x<45,45≤x<55,55≤x<65,65≤x<75,75≤x<85):
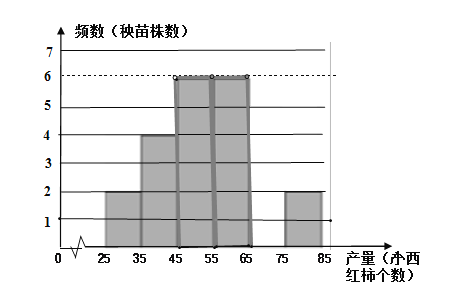
b.乙组数据在产量良好(45≤x<65)这两组的具体数据为: 46 46 47 47 48 48 55 57 57 57 58 61
c.数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 52.25 | 51 | 58 | 238 |
乙 | 52.25 | 57 | 210 |
(1)补全乙的频数分布直方图.
(2)写出表中![]() 的值.
的值.
(3)根据样本情况,估计乙大棚产量良好及以上的秧苗数为 株.
(4)根据抽样调查情况,可以推断出 大棚的小西红柿秧苗品种更适应市场需求,写出理由.(至少从两个不同的角度说明推断的合理性).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com