
����Ŀ��ijУ���꼶(2)���ڲ���У����˸߶ȵ���ѧ��У���һ���ͬѧ��������ֲ��������������ݲ��������д�����¡���ѧ����桷�е�һ���֣�
���� | ����У����˸߶� | ||
Ŀ�� | ������ѧ��ѧ֪ʶ����ѧ�������ʵ�����⩁����������˸߶� | ||
���� | ����һ | ������ | ������ |
ʾ��ͼ |
|
| |
�������� | Ƥ�ߡ������ | Ƥ�ߡ������ | |
�������� | AM��1.5m��AB��10m ������30����������60�� | AM��1.5m��AB��20m ������30����������60�� | |
�������(�� ����������) | �⣺ | �⣺ | |
(1)�����ڷ���һ������ѡһ�ַ���(��ѡ���ӷ�)�����ݷ����ṩ��ʾ��ͼ�����������д���еļ�����̡����������
(2)���������ѧ��֪ʶ�������һ�ֲ�ͬ�ڷ���һ�����IJ���������������ɱ����з�������������Ŀ����д��(Ҫ����ʾ��ͼ�б������IJ������ݳ�������ĸa��b��c����ʾ���Ƕ�����ĸ���������á���ʾ)
���𰸡�(1)����һ��DN��(![]() +1.5)m����������DN��(
+1.5)m����������DN��(![]() +1.5)m��(2)����������������DN��btan��+a��
+1.5)m��(2)����������������DN��btan��+a��
��������
��1������һ����Rt��ACD�У�AC��DCcot���� Rt��BCD�У�BC��DCcot������AB��AC��BC�г����̣��ⷽ�����DC��![]() m����DN��DC+CN��DC+AM�������DN�ij�������������Rt��ACD�У�AC��DCcot���� Rt��BCD�У�BC��DCcot������AB��AC+BC�г����̣��ⷽ�����DC��
m����DN��DC+CN��DC+AM�������DN�ij�������������Rt��ACD�У�AC��DCcot���� Rt��BCD�У�BC��DCcot������AB��AC+BC�г����̣��ⷽ�����DC��![]() m����DN��DC+CN��DC+AM�������DN�ij�����2����������ʾ��ͼ����ͼ����(��������)��Ƥ�ߡ�����ǣ�(��������)��AM��a��AC��b����DAC��������Rt��ACD�У�CD��btan������DN��DC+CN��AM��CN�����ɵ�DN��btan��+a�����𰸲�Ψһ��
m����DN��DC+CN��DC+AM�������DN�ij�����2����������ʾ��ͼ����ͼ����(��������)��Ƥ�ߡ�����ǣ�(��������)��AM��a��AC��b����DAC��������Rt��ACD�У�CD��btan������DN��DC+CN��AM��CN�����ɵ�DN��btan��+a�����𰸲�Ψһ��
�⣺����һ��
�⣺��Rt��ACD�У�AC��DCcot��
Rt��BCD��BC��DCcot����
��AB��AC��BC��
��(cot30����cot60��)DC��10��![]() DC��10��
DC��10��
���DC��![]() (m)��
(m)��
��AM��CN����DN��DC+CN��DC+AM��(![]() +1.5)(m)��
+1.5)(m)��
(���������)DN��(![]() +1.5)m��
+1.5)m��
��������
�⣺��Rt��ACD�У�AC��DCcot��
Rt��BCD��BC��DCcot����
��AB��AC+BC��
��(cot30��+cot60��)DC��20��(![]() )DC��20��
)DC��20��
���DC��![]() (m)��
(m)��
��AM��CN��
��DN��DC+CN��DC+AM��(![]() +1.5)(m)(���������)
+1.5)(m)(���������)
DN��(![]() +1.5)m��
+1.5)m��
������(��Ωһ)
ʾ��ͼ��
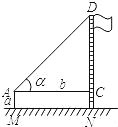
(��������)��Ƥ�ߡ�����ǣ�(��������)��AM��a��AC��b����DAC������
(�������)�⣺��Rt��ACD�У�CD��btan����
��DN��DC+CN��AM��CN��
��DN��btan��+a��
(�������)��DN��btan��+a��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
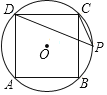
����Ŀ����ͼ��������ABCD�ڽ��ڡ�O��PΪ![]() ��һ�㣬����PD��PC��
��һ�㣬����PD��PC��
��1����CPD=______����
��2����DC=4��CP=2![]() ����DP�ij���
����DP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
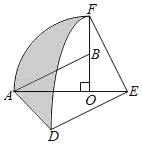
����Ŀ����ͼ����Rt��AOB�У���AOB=90�㣬OA=2��OB=1����Rt��AOB�Ƶ�O˳ʱ����ת90����õ�Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90����õ��߶�ED���քe��O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ���ֵ������__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=![]() x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��Pʱֱ��AC�·��������ϵĶ��㣮
x2+bx+c������ABC���������㣬���е�A��0��1������B����9��10����AC��x�ᣬ��Pʱֱ��AC�·��������ϵĶ��㣮

��1���������ߵĽ���ʽ����2������P����y��ƽ�е�ֱ��l��ֱ��AB��AC�ֱ��ڵ�E��F�����ı���AECP��������ʱ�����P�����ꣻ
��3������PΪ�����ߵĶ���ʱ����ֱ��AC���Ƿ���ڵ�Q��ʹ����C��P��QΪ��������������ABC���ƣ������ڣ������Q�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������ij����2000��������ײ��̳�����Ϊ�˹�������ܲ������������ﲶ�����������õ����±������ݣ�
������� | ƽ��ÿ��������� | |
��һ�β��� | 10 | 1.7ǧ�� |
�ڶ��β��� | 25 | 1.8ǧ�� |
�����β��� | 15 | 2.0ǧ�� |
����������������ijɻ�����95%����
(1)������������ƽ��ÿ����Լ����ǧ�ˣ�
(2)��������������ܲ����Ƕ���ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
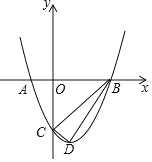
����Ŀ����ͼ��O������ԭ�㣬����A(��1��0)��������y��x2��bx��3��x�����һ������ΪB����y�ύ�ڵ�C���䶥��ΪD�㣮
(1)��b��ֵ�Լ���D�����ꣻ
(2)����BC��BD��CD����x�����Ƿ���ڵ�P��ʹ����A��C��PΪ��������������BCD���ƣ������ڣ������P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���ÿ����ǧԪ�ļ۸�һ����Ʒ����ÿ����Ʒ�ۼ�Ϊ360Ԫʱ��ÿ�¿��۳�100����ÿ������20%. Ϊ���������ۣ��̳�������ȡ�ʵ����۵ķ�ʽ�����������鷢�֣����ÿ����Ʒ����5Ԫ����ô�̳�ÿ�¾Ϳ��Զ��۳�15��.
��1������Ʒÿ���Ľ����Ƕ���Ԫ��
��2��Ҫʹ�̳�ÿ������������Ʒ������ﵽ6400Ԫ���Ҹ������ڼ��ٿ�棬��ÿ����ƷӦ���۶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС����ȫУ��Χ�������ȡ��һ����ѧ����������ζ̩�˩�������ϲ����̩����ʳ���������������ʾ���������Ƴ�����ͼ��ʾ�IJ�����������ͳ��ͼ������ͳ��ͼ��
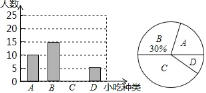
�����ʾ�����������̩����ʳ�У�����ϲ�����ǣ�����������ѡ��
A�������ձ� B������С���C��з������ D���������ı�
�����������Ϣ����������⣺
��1������������������������ ����
��2����ȫ����ͳ��ͼ������������ͳ��ͼ����A����������Ӧ��Բ�ĽǵĶ���Ϊ�� ����
��3����ȫУ��1200��ѧ���������ȫУѧ������ϲ����з����������ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ
Ϊ![]() ���ڽ������Σ�
���ڽ������Σ�![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() Ϊ
Ϊ![]() �����ߣ���
�����ߣ���![]() ���ӳ�����
���ӳ�����![]() .
.
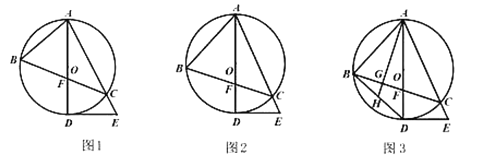
��1����֤��![]() ��
��
��2����ͼ����![]() ����֤��
����֤��![]() ��
��
��3����ͼ���ڣ�2���������£�����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ���ӳ��߽�
���ӳ��߽�![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com